
科目: 来源: 题型:
【题目】已知幂函数 ![]() 在(0,+∞)上为增函数,g(x)=f(x)+2
在(0,+∞)上为增函数,g(x)=f(x)+2 ![]()
(1)求m的值,并确定f(x)的解析式;
(2)对于任意x∈[1,2],都存在x1 , x2∈[1,2],使得f(x)≤f(x1),g(x)≤g(x2),若f(x1)=g(x2),求实数t的值;
(3)若2xh(2x)+λh(x)≥0对于一切x∈[1,2]成成立,求实数λ的取值范围.
查看答案和解析>>
科目: 来源: 题型:
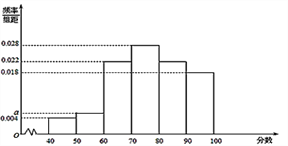
【题目】为响应国家治理环境污染的号召,增强学生的环保意识,宿州市某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了l00学生的成绩进行统计,成绩频率分布直方图如图所示.估计这次测试中成绩的众数为;平均数为;中位数为 . (各组平均数取中值计算,保留整数) 
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆C过两点M(﹣3,3),N(1,﹣5),且圆心在直线2x﹣y﹣2=0上
(1)求圆的方程;
(2)直线l过点(﹣2,5)且与圆C有两个不同的交点A、B,若直线l的斜率k大于0,求k的取值范围;
(3)在(2)的条件下,是否存在直线l使得弦AB的垂直平分线过点P(3,﹣1),若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}中各项都大于1,前n项和为Sn , 且满足an2+3an=6Sn﹣2.
(1)求数列{an}的通项公式;
(2)令bn= ![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(3)求使得Tn< ![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是矩形,侧面PAD丄底面ABCD,∠APD= ![]() . (I )求证:平面PAB丄平面PCD;
. (I )求证:平面PAB丄平面PCD;
(II)如果AB=BC,PB=PC,求二面角B﹣PC﹣D的余弦值.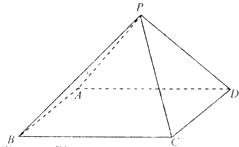
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接党的“十九”大的召开,某校组织了“歌颂祖国,紧跟党走”党史知识竞赛,从参加考试的学生中抽出50名学生,将其成绩(满分100分,成绩均为整数)分成六段![]() ,
, ![]() ,…,
,…, ![]() 后绘制频率分布直方图(如下图所示)
后绘制频率分布直方图(如下图所示)
(Ⅰ)求频率分布图中![]() 的值;
的值;
(Ⅱ)估计参加考试的学生得分不低于80的概率;
(Ⅲ)从这50名学生中,随机抽取得分在![]() 的学生2人,求此2人得分都在
的学生2人,求此2人得分都在![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2 ![]() ,PA=4且E为PB的中点.
,PA=4且E为PB的中点. 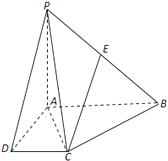
(1)求证:CE∥平面PAD;
(2)求直线CE与平面PAC所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点. 
(1)证明:MN∥平面PAB;
(2)求点M到平面PBC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com