
【题目】为迎接党的“十九”大的召开,某校组织了“歌颂祖国,紧跟党走”党史知识竞赛,从参加考试的学生中抽出50名学生,将其成绩(满分100分,成绩均为整数)分成六段![]() ,
, ![]() ,…,
,…, ![]() 后绘制频率分布直方图(如下图所示)
后绘制频率分布直方图(如下图所示)
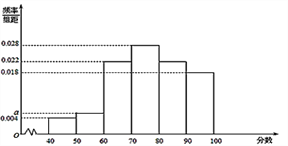
(Ⅰ)求频率分布图中![]() 的值;
的值;
(Ⅱ)估计参加考试的学生得分不低于80的概率;
(Ⅲ)从这50名学生中,随机抽取得分在![]() 的学生2人,求此2人得分都在
的学生2人,求此2人得分都在![]() 的概率.
的概率.
【答案】(Ⅰ)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由频率和为1,列方程可求出![]() ;(2)用样本得分不低于80的频率估计参加考试的学生得分不低于80的概率,(3)通过列举出所有可能结果,应用古典概型概率计算方法求出概率.
;(2)用样本得分不低于80的频率估计参加考试的学生得分不低于80的概率,(3)通过列举出所有可能结果,应用古典概型概率计算方法求出概率.
试题解析:(Ⅰ)因为![]() ,所以
,所以![]()
(Ⅱ)由所给频率分布直方图知,50名学生得分不低于80的频率为![]() ,
,
所以参加考试的学生得分不低于80的概率的估计值为![]() .
.
(Ⅲ)所抽出的50名学生得分在[50,60)的有:50×0.006×10=3(人),即为![]() ;
;
得分在[40,50)的有: 50×0.004×40=2(人),即为![]() .
.
从这5名学生中随机抽取2人,所有可能的结果共有10种,它们是![]()
![]() 又因为所抽取2人的评分都在[40,50)的结果有1种,即
又因为所抽取2人的评分都在[40,50)的结果有1种,即![]() ,故所求的概率为
,故所求的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点在平面直角坐标系的原点![]() 处,极轴与
处,极轴与![]() 轴的正半轴重合,且长度单位相同;曲线
轴的正半轴重合,且长度单位相同;曲线![]() 的方程是
的方程是![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),设
),设![]() , 直线
, 直线![]() 与曲线
与曲线![]() 交于
交于 ![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长度;
的长度;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合M={(x,y)|y= ![]() },N={(x,y)|x﹣y+m=0},若M∩N的子集恰有4个,则m的取值范围是( )
},N={(x,y)|x﹣y+m=0},若M∩N的子集恰有4个,则m的取值范围是( )
A.(﹣2 ![]() ,2
,2 ![]() )
)
B.[﹣2,2 ![]() )
)
C.(﹣2 ![]() ,﹣2]
,﹣2]
D.[2,2 ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() 曲线
曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家治理环境污染的号召,增强学生的环保意识,宿州市某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛,为了解本次竞赛的成绩情况,从中抽取了l00学生的成绩进行统计,成绩频率分布直方图如图所示.估计这次测试中成绩的众数为;平均数为;中位数为 . (各组平均数取中值计算,保留整数) 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过抛物线C的焦点,且与C的对称轴垂直.l与C交于A,B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为( )
A.18
B.24
C.36
D.48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点O,![]() 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为![]() ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为![]() ,圆C的半径为4.
,圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列算式:13=1,23=3+5,33=7+9+11,43=13+15+17+19,…若某数n3按上述规律展开后,发现右边含有“2017”这个数,则:n= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com