
科目: 来源: 题型:
【题目】某电影院共有1000个座位,票价不分等次,根据电影院的经营经验,当每张票价不超过10元时,票可全部售出;当票价高于10元时,每提高1元,将有30张票不能售出.为了获得更好的收益,需要给电影院一个合适的票价,基本条件是:①为了方便找零和算账,票价定为1元的整数倍;②电影院放映一场电影的成本是5750元,票房收入必须高于成本.用x(元)表示每张票价,用y(元)表示该电影放映一场的纯收入(除去成本后的收入). (Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)票价定为多少时,电影放映一场的纯收入最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】袋中装着标有数字1、2、3、4、5的小球各2个,从袋中任取3个小球,每个小球被取出的可能性都相等,用ξ表示取出的3个小球上的最大数字,求:
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量ξ的概率分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=PA=4,A点在PD上的射影为G点,E点在AB上,平面PCE⊥平面PCD. 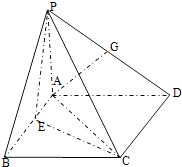
(1)求证:AG⊥平面PCD;
(2)求直线PD与平面PCE所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设离心率为 ![]() 的椭圆
的椭圆![]() 的左、右焦点为
的左、右焦点为![]() , 点P是E上一点,
, 点P是E上一点, ![]() ,
, ![]() 内切圆的半径为
内切圆的半径为 ![]() .
.
(1)求E的方程;
(2)矩形ABCD的两顶点C、D在直线![]() 上,A、B在椭圆E上,若矩形ABCD的周长为
上,A、B在椭圆E上,若矩形ABCD的周长为 ![]() , 求直线AB的方程.
, 求直线AB的方程.
查看答案和解析>>
科目: 来源: 题型:
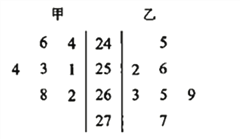
【题目】双十一网购狂欢,快递业务量猛增.甲、乙两位快递员![]() 月
月![]() 日到
日到![]() 日每天送件数量的茎叶图如图所示.
日每天送件数量的茎叶图如图所示.
(Ⅰ)根据茎叶图判断哪个快递员的平均送件数量较多(写出结论即可);
(Ⅱ)求甲送件数量的平均数;
(Ⅲ)从乙送件数量中随机抽取![]() 个,求至少有一个送件数量超过甲的平均送件数量的概率.
个,求至少有一个送件数量超过甲的平均送件数量的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线f(x)= ![]() (x>0)上有一点列Pn(xn , yn)(n∈N*),过点Pn在x轴上的射影是Qn(xn , 0),且x1+x2+x3+…+xn=2n+1﹣n﹣2.(n∈N*)
(x>0)上有一点列Pn(xn , yn)(n∈N*),过点Pn在x轴上的射影是Qn(xn , 0),且x1+x2+x3+…+xn=2n+1﹣n﹣2.(n∈N*)
(1)求数列{xn}的通项公式;
(2)设四边形PnQnQn+1Pn+1的面积是Sn , 求Sn;
(3)在(2)条件下,求证: ![]() +
+ ![]() +…+
+…+ ![]() <4.
<4.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2 ![]() .
. 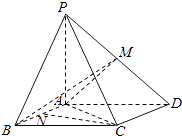
(1)求证:CD⊥平面PAC;
(2)如果如果N是棱AB上一点,且直线CN与平面MAB所成角的正弦值为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某投资公司计划投资A,B两种金融产品,根据市场调查与预测,A产品的利润y1与投资金额x的函数关系为y1=18﹣ ![]() ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2= ![]() (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).
(1)该公司已有100万元资金,并全部投入A,B两种产品中,其中x万元资金投入A产品,试把A,B两种产品利润总和表示为x的函数,并写出定义域;
(2)在(1)的条件下,试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com