
科目: 来源: 题型:
【题目】已知 ![]() ,
, ![]() .
.
(1)当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2)由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆 ![]() 的左顶点和上顶点分别为A、B,左、右焦点分别是F1 , F2 , 在线段AB上有且只有一个点P满足PF1⊥PF2 , 则椭圆的离心率为( )
的左顶点和上顶点分别为A、B,左、右焦点分别是F1 , F2 , 在线段AB上有且只有一个点P满足PF1⊥PF2 , 则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某省的一个气象站观测点在连续4天里记录的![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位:
(单位: ![]() )的情况如表1:
)的情况如表1:
|
| 700 |
|
|
| 0.5 | 3.5 | 6.5 | 9.5 |
该省某市2017年9月![]() 指数频数分布如表2:
指数频数分布如表2:
|
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)小李在该市开了一家洗车店,经统计,洗车店平均每天的收入与![]() 指数有相关关系,如表3:
指数有相关关系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根据表3估计小李的洗车店9月份平均每天的收入.
(附参考公式: ![]() ,其中
,其中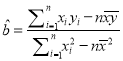 ,
, ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四边形ABCD满足AD∥BC,BA=AD=DC= ![]() BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使面B1AE⊥面AECD,F,G分别为B1D,AE的中点.
BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使面B1AE⊥面AECD,F,G分别为B1D,AE的中点. 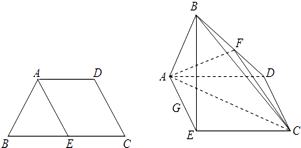
(1)求三棱锥E﹣ACB1的体积;
(2)证明:B1E∥平面ACF;
(3)证明:平面B1GD⊥平面B1DC.
查看答案和解析>>
科目: 来源: 题型:
【题目】矩形ABCD中,AD=2,AB=4,E,F分别为边AB,AD的中点,将△ADE沿DE折起,点A,F折起后分别为点A′,F′,得到四棱锥A′﹣BCDE.给出下列几个结论:
①A′,B,C,F′四点共面;
②EF'∥平面A′BC;
③若平面A′DE⊥平面BCDE,则CE⊥A′D;
④四棱锥A′﹣BCDE体积的最大值为 ![]() .
.
其中正确的是(填上所有正确的序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】不等式2x2﹣x﹣3>0解集为( )
A.{x|﹣1<x< ![]() }??
}??
B.{x|x> ![]() 或x<﹣1}??
或x<﹣1}??
C.{x|﹣ ![]() <x<1}??
<x<1}??
D.{x|x>1或x<﹣ ![]() }
}
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A(0,2)为圆C:x2+y2﹣2ax﹣2ay=0(a>0)外一点,圆C上存在点P使得∠CAP=45°,则实数a的取值范围是( )
A.(0,1)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,g(x)=ax,(a∈R).
(1)若函数y=f(x)是偶函数,求出符合条件的实数a的值;
(2)若方程f(x)=g(x)有两解,求出实数a的取值范围;
(3)若a>0,记F(x)=g(x)f(x),试求函数y=F(x)在区间[1,2]上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com