
科目: 来源: 题型:
【题目】给出如下几个结论:①命题“x∈R,sinx+cosx=2”的否定是“x∈R,sinx+cosx≠2”;②命题“x∈R,sinx+ ![]() ≥2”的否定是“x∈R,sinx+
≥2”的否定是“x∈R,sinx+ ![]() <2”;③对于x∈(0,
<2”;③对于x∈(0, ![]() ),tanx+
),tanx+ ![]() ≥2;
≥2;
④x∈R,使sinx+cosx= ![]() .其中正确的为( )
.其中正确的为( )
A.③
B.③④
C.②③④
D.①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某工厂每天固定成本是4万元,每生产一件产品成本增加100元,工厂每件产品的出厂价定为![]() 元时,生产
元时,生产![]() 件产品的销售收入是
件产品的销售收入是![]() (元),
(元),![]() 为每天生产
为每天生产![]() 件产品的平均利润(平均利润=总利润/总产量).销售商从工厂每件
件产品的平均利润(平均利润=总利润/总产量).销售商从工厂每件![]() 元进货后又以每件
元进货后又以每件![]() 元销售,
元销售, ![]() ,其中
,其中![]() 为最高限价
为最高限价![]() ,
, ![]() 为销售乐观系数,据市场调查,
为销售乐观系数,据市场调查, ![]() 是由当
是由当![]() 是
是![]() ,
, ![]() 的比例中项时来确定.
的比例中项时来确定.
(1)每天生产量![]() 为多少时,平均利润
为多少时,平均利润![]() 取得最大值?并求
取得最大值?并求![]() 的最大值;
的最大值;
(2)求乐观系数![]() 的值;
的值;
(3)若![]() ,当厂家平均利润最大时,求
,当厂家平均利润最大时,求![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代太极图是一种优美的对称图.如果一个函数的图像能够将圆的面积和周长分成两个相等的部分,我们称这样的函数为圆的“太极函数”.下列命题中错误命题的个数是( )
![]() 对于任意一个圆其对应的太极函数不唯一;
对于任意一个圆其对应的太极函数不唯一;
![]() 如果一个函数是两个圆的太极函数,那么这两个圆为同心圆;
如果一个函数是两个圆的太极函数,那么这两个圆为同心圆;
![]() 圆
圆![]() 的一个太极函数为
的一个太极函数为![]() ;
;
![]() 圆的太极函数均是中心对称图形;
圆的太极函数均是中心对称图形;
![]() 奇函数都是太极函数;
奇函数都是太极函数;
![]() 偶函数不可能是太极函数.
偶函数不可能是太极函数.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.
(1)证明:直线OM的斜率与l的斜率的乘积为定值;
(2)若l过点( ![]() ,m),延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率;若不能,说明理由.
,m),延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率;若不能,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知向量 ![]() =(an , 2n),
=(an , 2n), ![]() =(2n+1 , ﹣an+1),n∈N* , 向量
=(2n+1 , ﹣an+1),n∈N* , 向量 ![]() 与
与 ![]() 垂直,且a1=1
垂直,且a1=1
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=log2an+1,求数列{anbn}的前n项和Sn .
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,边a、b、c分别是角A、B、C的对边,且满足bcosC=(3a﹣c)cosB.
(1)求cosB;
(2)若 ![]()
![]() =4,b=4
=4,b=4 ![]() ,求边a,c的值.
,求边a,c的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 分别是椭圆
分别是椭圆![]() 的长轴与短轴的一个端点,
的长轴与短轴的一个端点, ![]() 是椭圆的左、右焦点,以
是椭圆的左、右焦点,以![]() 点为圆心、3为半径的圆与以
点为圆心、3为半径的圆与以![]() 点为圆心、1为半径的圆的交点在椭圆
点为圆心、1为半径的圆的交点在椭圆![]() 上,且
上,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上一点,直线
上一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为了制定合理的节电方案,对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:百千瓦![]() 时),将数据按
时),将数据按![]()
![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
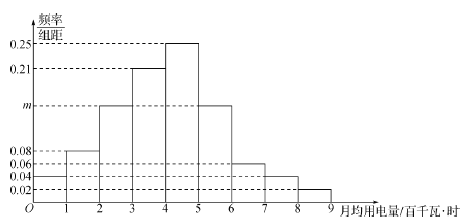
(1)求直方图中![]() 的值;
的值;
(2)设该市有100万户居民,估计全市每户居民中月均用电量不低于6百千瓦![]() 时的人数及每户居民月均用电量的中位数;
时的人数及每户居民月均用电量的中位数;
(3)政府计划对月均用电量在4百千瓦![]() 时以下的用户进行奖励,月均用电量在
时以下的用户进行奖励,月均用电量在![]() 内的用户奖励20元/月,月均用电量在
内的用户奖励20元/月,月均用电量在![]() 内的用户奖励10元/月,月均用电量在
内的用户奖励10元/月,月均用电量在![]() 内的用户奖励2元/月.若该市共有400万户居民,试估计政府执行此计划的年度预算.
内的用户奖励2元/月.若该市共有400万户居民,试估计政府执行此计划的年度预算.
查看答案和解析>>
科目: 来源: 题型:
【题目】设向量 ![]() =(
=( ![]() sinx,sinx),
sinx,sinx), ![]() =(cosx,sinx),x∈[0,
=(cosx,sinx),x∈[0, ![]() ]
]
(1)若| ![]() |=|
|=| ![]() |,求x的值;
|,求x的值;
(2)设函数f(x)= ![]()
![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目: 来源: 题型:
【题目】在极坐标系中,曲线![]() ,曲线
,曲线![]() .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为![]() 轴正半轴建立平面直角坐标系
轴正半轴建立平面直角坐标系![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为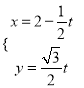 (
(![]() 为参数).
为参数).
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 与
与![]() 交于不同的四点,这四点在
交于不同的四点,这四点在![]() 上排列顺次为
上排列顺次为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com