【题目】已知数列{an}的前n项和是Sn ， 且Sn+ an=1（n∈N*）．
（1）求数列{an}的通项公式；
（2）设bn=log4（1﹣Sn+1）（n∈N*），Tn= + +…+ ，求使Tn≥ 成立的最小的正整数n的值．

（1）当9天购买一次配料时，求该厂用于配料的保管费用是多少元？

（2）设该厂天购买一次配料，求该厂在这天中用于配料的总费用（元）关于的函数关系式，并求该厂多少天购买一次配料才能使平均每天支付的费用最少？

【题目】已知二次函数，关于实数的不等式的解集为．

（1）当时，解关于的不等式： ；

（2）是否存在实数，使得关于的函数（）的最小值为？若存在，求实数的值；若不存在，说明理由．

【题目】已知圆 ，圆 ．
（1）求两圆公共弦所在直线的方程；
（2）直线ι过点（4，﹣4）与圆C1相交于A，B两点，且 ，求直线ι的方程．

【题目】如图，在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形，现有均匀的粒子散落在正方形中，问粒子落在中间带形区域的概率是多少？

【题目】已知函数．

（1）当时，求函数的单调区间；

（2）若函数既有一个极小值又有一个极大值，求的取值范围；

（3）若存在，使得当时， 的值域是，求的取值范围．

【题目】已知数列中， ，且对任意正整数都成立，数列的前项和为．

（1）若，且，求；

（2）是否存在实数，使数列是公比为1的等比数列，且任意相邻三项按某顺序排列后成等差数列，若存在，求出所有的值；若不存在，请说明理由；

（3）若，求．（用表示）．

（1）填出表中所剩的空格；
（2）画出频率分布直方图．

【题目】如图，三棱锥P﹣ABC中，PB⊥底面ABC，∠BCA=90°，PB=BC=CA=2，E为PC的中点，M为AB的中点，点F在PA上，且2PF=FA．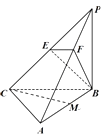

（1）求证：BE⊥平面PAC；
（2）求证：CM∥平面BEF；
（3）求平面ABC与平面BEF所成的二面角的平面角（锐角）的余弦值．

【题目】在△ABC中，内角A，B，C所对的边分别为a，b，c，且a+b+c=16．
（1）若a=4，b=5，求cosC的值；
（2）若sinA+sinB=3sinC，且△ABC的面积S=18sinC，求a和b的值．