
科目: 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,给出以下结论: ①直线A1B与B1C所成的角为60°;
②若M是线段AC1上的动点,则直线CM与平面BC1D所成角的正弦值的取值范围是 ![]() ;
;
③若P,Q是线段AC上的动点,且PQ=1,则四面体B1D1PQ的体积恒为 ![]() .
.
其中,正确结论的个数是( )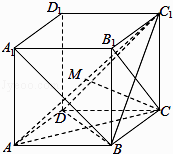
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目: 来源: 题型:
【题目】在班级的演讲比赛中,将甲、乙两名同学的得分情况制成如图所示的茎叶图.记甲、乙两名同学所得分数的平均分分别为 ![]() 甲、
甲、 ![]() 乙 , 则下列判断正确的是( )
乙 , 则下列判断正确的是( ) 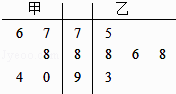
A.![]() 甲<
甲< ![]() 乙 , 甲比乙成绩稳定
乙 , 甲比乙成绩稳定
B.![]() 甲>
甲> ![]() 乙,甲比乙成绩稳定
乙,甲比乙成绩稳定
C.![]() 甲<
甲< ![]() 乙 , 乙比甲成绩稳定
乙 , 乙比甲成绩稳定
D.![]() 甲>
甲> ![]() 乙 , 乙比甲成绩稳定
乙 , 乙比甲成绩稳定
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的左、右焦点分别为F1、F2 , 离心率e=
(a>b>0)的左、右焦点分别为F1、F2 , 离心率e= ![]() ,与双曲线
,与双曲线 ![]() 有相同的焦点. (I)求椭圆C的标准方程;
有相同的焦点. (I)求椭圆C的标准方程;
(II)过点F1的直线l与该椭圆C交于M、N两点,且| ![]() +
+ ![]() N|=
N|= ![]() ,求直线l的方程.
,求直线l的方程.
(Ⅲ)是否存在圆心在原点的圆,使得该圆的任一条切线与椭圆C有两个交点A、B,且OA⊥OB?若存在,写出该圆的方程,否则,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60° 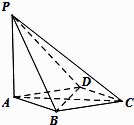
(1)若PA=AB,求PB与平面PDC所成角的正弦值;
(2)当平面PBC与平面PDC垂直时,求PA的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点P(x,y)在圆x2+y2﹣6x﹣6y+14=0上
(1)求 ![]() 的最大值和最小值;
的最大值和最小值;
(2)求x2+y2+2x+3的最大值与最小值;
(3)求x+y的最大值与最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=sin(2x+φ1),g(x)=cos(4x+φ2),|φ1|≤ ![]() ,|φ2|≤
,|φ2|≤ ![]() . 命题①:若直线x=φ是函数f(x)和g(x)的对称轴,则直线x=
. 命题①:若直线x=φ是函数f(x)和g(x)的对称轴,则直线x= ![]() kπ+φ(k∈Z)是函数g(x)的对称轴;
kπ+φ(k∈Z)是函数g(x)的对称轴;
命题②:若点P(φ,0)是函数f(x)和g(x)的对称中心,则点Q( ![]() +φ,0)(k∈Z)是函数f(x)的中心对称.( )
+φ,0)(k∈Z)是函数f(x)的中心对称.( )
A.命题①②都正确
B.命题①②都不正确
C.命题①正确,命题②不正确
D.命题①不正确,命题②正确
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC. (Ⅰ)求直线PC与平面ABC所成角的大小;
(Ⅱ)求二面角B﹣AP﹣C的大小.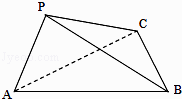
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=a(|sinx|+|cosx|)﹣ ![]() sin2x﹣1,若f(
sin2x﹣1,若f( ![]() )=
)= ![]() ﹣
﹣ ![]() .
.
(1)求a的值,并写出函数f(x)的最小正周期(不需证明);
(2)是否存在正整数k,使得函数f(x)在区间[0,kπ]内恰有2017个零点?若存在,求出k的值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l1的方程为3x+4y﹣12=0,
(1)求l2的方程,使得:①l2与l1平行,且过点(﹣1,3); ②l2与l1垂直,且l2与两坐标轴围成的三角形面积为4;
(2)直线l1与两坐标轴分别交于A、B 两点,求三角形OAB(O为坐标原点)内切圆及外接圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com