
科目: 来源: 题型:
【题目】如图,在平面四边形ABCD中,AD=1,CD=2,AC= ![]() .
. 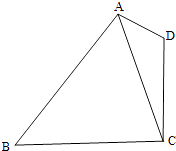
(1)求cos∠CAD的值;
(2)若cos∠BAD=﹣ ![]() ,sin∠CBA=
,sin∠CBA= ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列各组中的函数f(x),g(x)表示同一函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)=x+1,g(x)= ![]()
C.f(x)=|x|,g(x)= ![]()
D.f(x)=log22x , g(x)=2log2x
查看答案和解析>>
科目: 来源: 题型:
【题目】某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示: (Ⅰ)分别计算两组数据的平均数,并比较哪个班级的客观题平均成绩更好;
(Ⅱ)从这两组数据各取两个数据,求其中至少有2个满分(60分)的概率;
(Ⅲ)规定客观题成绩不低于55分为“优秀客观卷”,以这20人的样本数据来估计此次高三数学模拟的总体数据,若从总体中任选4人,记X表示抽到“优秀客观卷”的学生人数,求X的分布列及数学期望.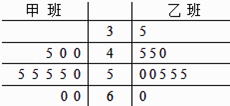
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究.全年级共有1350人,男女生比例为8:7,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为 ![]() ,通过对被抽取学生的问卷调查,得到如下2x2列联表:
,通过对被抽取学生的问卷调查,得到如下2x2列联表:
支持 | 反对 | 总计 | |
男生 | 30 | ||
女生 | 25 | ||
总计 |
(Ⅰ)完成列联表,并判断能否有99.9%的把握认为态度与性别有关?
(Ⅱ)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界表:K2= ![]()
P(K2≥k0) | 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
k0 | 2.706% | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=(x﹣1)|x﹣a|﹣x﹣2a(x∈R).
(1)若a=﹣1,求方程f(x)=1的解集;
(2)若 ![]() ,试判断函数y=f(x)在R上的零点个数,并求此时y=f(x)所有零点之和的取值范围.
,试判断函数y=f(x)在R上的零点个数,并求此时y=f(x)所有零点之和的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】一辆汽车在某段路程中的行驶速率与时间的关系如图所示. 
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车在行驶该段路程前里程表的读数是8018km,试求汽车在行驶这段路程时里程表读数s(km)与时间t (h)的函数解析式,并作出相应的图象.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)(﹣π<φ<0,ω>0)的图象关于直线 ![]() 对称,且两相邻对称中心之间的距离为
对称,且两相邻对称中心之间的距离为 ![]() .
.
(1)求函数y=f(x)的单调递增区间;
(2)若关于x的方程f(x)+log2k=0在区间 ![]() 上总有实数解,求实数k的取值范围.
上总有实数解,求实数k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下: (Ⅰ)根据频率分布直方图,求a的值,并估计众数,说明此众数的实际意义;
(Ⅱ)从“能接受的最高票价”落在[8,10),[10,12]的被调查者中各随机选取3人进行追踪调查,记选中的6人中35岁以上(含35岁)的人数为X,求随机变量X的分布列及数学期望.
最高票价 | 35岁以下人数 |
[2,4) | 2 |
[4,6) | 8 |
[6,8) | 12 |
[8,10) | 5 |
[10,12] | 3 |
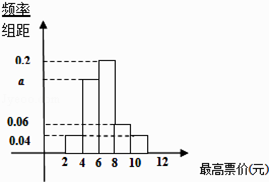
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x+ ![]() ,g(x)=f2(x)﹣af(x)+2a有四个不同的零点x1 , x2 , x3 , x4 , 则[2﹣f(x1)][2﹣f(x2)][2﹣f(x3)][2﹣f(x4)]的值为 .
,g(x)=f2(x)﹣af(x)+2a有四个不同的零点x1 , x2 , x3 , x4 , 则[2﹣f(x1)][2﹣f(x2)][2﹣f(x3)][2﹣f(x4)]的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com