【题目】如图，在平面直角坐标系xoy中，A为以原点O为圆心的单位圆O与x正半轴的交点，在圆心角为 的扇形AOB的弧AB上任取一点 P，作 PN⊥OA于N，连结PO，记∠PON=θ．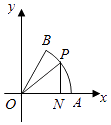
（1）设△PON的面积为y，使y取得最大值时的点P记为E，点N记为F，求此时 的值；
（2）求k=a| || |+ （a∈R，E 是在（1）条件下的点 E）的值域．

【题目】四名选手 A、B、C、D 参加射击、抛球、走独木桥三项比赛，每个选手在各项比赛中获得合格、不合格机会相等，比赛结束，评委们会根据选手表现给每位选手评定比赛成绩，根据比赛成绩，对前两名进行奖励．
（1）选手 D 至少获得两个合格的概率；
（2）选手 C、D 只有一人得到奖励的概率．

【题目】 =（3 sinx， cosx）， =（cosx， cosx），f （x）= ．
（1）求f（x）的单调递减区间；
（2）x∈[﹣ ， ]时，g（x）=f（x）+m的最大值为 ，求g（x）的最小值及相应的x值．

（1）在规定的坐标系中，画出 x，y 的散点图；
（2）求y与x之间的回归方程，并预测40秒时的深度（回归方程精确到小数点后两位；预测结果精确到整数）． 回归方程： =bx+a，其中 = ，a= ﹣b ．

【题目】已知 ， ， 是同一平面内的三个向量，其中 =（﹣ ，1）．
（1）若| |=2 且 ∥ ，求 的坐标；
（2）若| |= ，（ +3 ）⊥（ ﹣ ），求向量 ， 的夹角的余弦值．

【题目】解答题。
（1）如图，证明命题“a是平面π内的一条直线，b是π外的一条直线（b不垂直于π），c是直线b在π上的投影，若a⊥b，则a⊥c”为真．
（2）写出上述命题的逆命题，并判断其真假（不需要证明）

【题目】设命题P：实数x满足2x2﹣5ax﹣3a2＜0，其中a＞0，命题q：实数x满足 ．
（1）若a=2，且p∧q为真，求实数x的取值范围；
（2）若￢p是￢q的充分不必要条件，求实数a的取值范围．

【题目】已知圆M：x2+（y﹣4）2=4，点P是直线l：x﹣2y=0上的一动点，过点P作圆M的切线PA，PB，切点为A，B．
（1）当切线PA的长度为 时，求点P的坐标；
（2）若△PAM的外接圆为圆N，试问：当P在直线l上运动时，圆N是否过定点？若存在，求出所有的定点的坐标；若不存在，说明理由．
（3）求线段AB长度的最小值．

【题目】已知曲线C的方程为：ax2+ay2﹣2a2x﹣4y=0（a≠0，a为常数）．
（1）判断曲线C的形状；
（2）设曲线C分别与x轴、y轴交于点A、B（A、B不同于原点O），试判断△AOB的面积S是否为定值？并证明你的判断；
（3）设直线l：y=﹣2x+4与曲线C交于不同的两点M、N，且|OM|=|ON|，求曲线C的方程．

【题目】若α，β∈（0， ），sin（ ）=﹣ ，cos（ ）= ，则α+β= ．