【题目】在二项式（ + ）n展开式中，前三项的系数成等差数列． 求：（1）展开式中各项系数和；
【答案】解：由题意得2 × =1+ × ，
化为：n2﹣9n+8=0，解得n=1（舍去）或8．
∴n=8．
在 中，令x=1，可得展开式中各项系数和= = ．
（1）展开式中系数最大的项．

【题目】已知函数f（x）=x3﹣3x2﹣9x+2．
（1）求函数f（x）的单调区间；
（2）求函数f（x）在区间[﹣1，m]（m＞﹣1）的最小值．

经检验，这组样本数据具有线性相关关系，那么对于加工零件的个数x与加工时间y这两个变量，下列判断正确的是（ ）
A.成正相关，其回归直线经过点（30，75）
B.成正相关，其回归直线经过点（30，76）
C.成负相关，其回归直线经过点（30，76）
D.成负相关，其回归直线经过点（30，75）

(1)求证：对任意x1，x2∈[－1，1]，有[f(x1)＋f(x2)]·(x1＋x2)≤0；

(2)若f(1－a)＋f(1－a2)＜0，求实数a的取值范围．

【题目】某电视台举行电视奥运知识大奖赛，比赛分初赛和决赛两部分．为了增加节目的趣味性，初赛采用选手选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累计答对3题或答错3题即终止其初赛的比赛，答对3题者直接进入决赛，答错3题者则被淘汰．已知选手甲答题的正确率为 ． （Ⅰ）求选手甲可进入决赛的概率；
（Ⅱ）设选手甲在初赛中答题的个数为ξ，试写出ξ的分布列，并求ξ的数学期望．

求证：(1) BE∥平面PAD；

(2) 平面BEF⊥平面PCD.

设某旅游景点每天的固定成本为500元，门票每张为30元，变动成本与购票进入旅游景点的人数的算术平方根成正比。一天购票人数为25时，该旅游景点收支平衡；一天购票人数超过100时，该旅游景点须另交保险费200元。设每天的购票人数为，盈利额为元。

（Ⅰ）求与之间的函数关系；

（Ⅱ）该旅游景点希望在人数达到20人时即不出现亏损，若用提高门票价格的措施，则每张门票至少要多少元（取整数）？

（参考数据：.）

(1)点A(5，0)到直线l的距离为3，求直线l的方程；

(2)求点A(5，0)到直线l的距离的最大值．

【题目】人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律，可以为有效控制人口增长提供依据.早在1798年，英国经济学家马尔萨斯（T.R.Malthus，1766—1834）就提出了自然状态下的人口增长模型： ，其中x表示经过的时间， 表示x=0时的人口，r表示人口的平均增长率.

下表是1950―1959年我国人口数据资料：

如果以各年人口增长率的平均值作为我国这一时期的人口增长率，用马尔萨斯人口增长模型建立我国这一时期的具体人口增长模型，某同学利用图形计算器进行了如下探究：

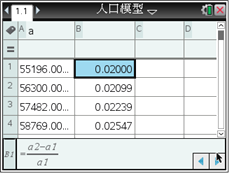
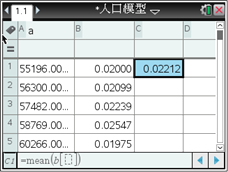
由此可得到我国1950―1959年我国这一时期的具体人口增长模型为____________. （精确到0.001）

【题目】甲、乙俩人各进行3次射击，甲每次击中目标的概率为 ，乙每次击中目标的概率为 ． （Ⅰ）记甲恰好击中目标2次的概率；
（Ⅱ）求乙至少击中目标2次的概率；
（Ⅲ）求乙恰好比甲多击中目标2次的概率；