【题目】已知常数a＞0，函数f（x）=ln（1+ax）﹣ ．
（Ⅰ）讨论f（x）在区间（0，+∞）上的单调性；
（Ⅱ）若f（x）存在两个极值点x1 ， x2 ， 且f（x1）+f（x2）＞0，求a的取值范围．

【题目】设数列{an}的前n项和为Sn ． 若Sn=2an﹣n，则 + + + = ．

【题目】为了调查中小学课外使用互联网的情况，教育部向华东、华北、华南和西部地区60所中小学发出问卷份， 名学生参加了问卷调查，并根据所得数据画出样本的频率分布直方图（如图）.

（1）要从这名中小学中用分层抽样的方法抽取名中小学生进一步调查，则在（小时）时间段内应抽出的人数是多少？

（2）若希望的中小学生每天使用互联网时间不少于（小时），请估计的值，并说明理由.

【题目】已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A、B两点．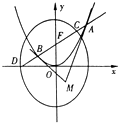
（1）设抛物线在A、B处的切线的交点为M，若点M的横坐标为2，求△ABM的外接圆方程．
（2）若直线l与椭圆 + =1的交点为C，D，问是否存在这样的直线l使|AF||CF|=|BF||DF|，若存在，求出l的方程；若不存在，说明理由．

【题目】设点P在△ABC的BC边所在的直线上从左到右运动，设△ABP与△ACP的外接圆面积之比为λ，当点P不与B，C重合时，（ ）
A.λ先变小再变大
B.当M为线段BC中点时，λ最大
C.λ先变大再变小
D.λ是一个定值

【题目】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．如图，在阳马P﹣ABCD中，侧棱PD⊥底面ABCD，且PD=CD，过棱PC的中点E，作EF⊥PB交PB于点F，连接DE，DF，BD，BE．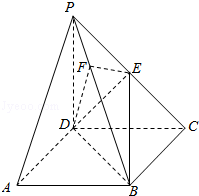
（1）证明：PB⊥平面DEF．试判断四面体DBEF是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由；
（2）若面DEF与面ABCD所成二面角的大小为 ，求 的值．

为了解参赛学生的数独水平，该科技馆采用分层抽样的方法从这四所中学的参赛学生中抽取30名参加问卷调查．
（Ⅰ）问甲、乙、丙、丁四所中学各抽取多少名学生？
（Ⅱ）从参加问卷调查的30名学生中随机抽取2名，求这2名学生来自同一所中学的概率；
（Ⅲ）在参加问卷调查的30名学生中，从来自甲、丙两所中学的学生中随机抽取2名，用X表示抽得甲中学的学生人数，求X的分布列．

【题目】已知△ABC的外接圆半径为1，角A，B，C的对边分别为a，b，c，且2acos A=ccos B+bcos C．
（Ⅰ）求A；
（Ⅱ）若b2+c2=7，求△ABC的面积．

【题目】设F为双曲线 ﹣ =1（a＞b＞0）的右焦点，过点F的直线分别交两条渐近线于A，B两点，OA⊥AB，若2|AB|=|OA|+|OB|，则该双曲线的离心率为（ ）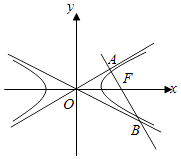

A.
B.2
C.
D.

【题目】设函数f（x）=2017x+sin2017x，g（x）=log2017x+2017x ， 则（ ）
A.对于任意正实数x恒有f（x）≥g（x）
B.存在实数x0 ， 当x＞x0时，恒有f（x）＞g（x）
C.对于任意正实数x恒有f（x）≤g（x）
D.存在实数x0 ， 当x＞x0时，恒有f（x）＜g（x）