
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE. 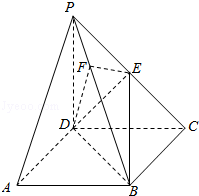
(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(2)若面DEF与面ABCD所成二面角的大小为 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)证明:解法1:因为PD⊥底面ABCD,所以PD⊥BC,
由底面ABCD为长方形,有BC⊥CD,而PD∩CD=D,
所以BC⊥平面PCD.而DE平面PDC,所以BC⊥DE.
又因为PD=CD,点E是PC的中点,所以DE⊥PC.
而PC∩CB=C,所以DE⊥平面PBC.而PB平面PBC,所以PB⊥DE.
又PB⊥EF,DE∩FE=E,所以PB⊥平面DEF.
由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,
即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB
解法2:
以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系.设PD=DC=1,BC=λ,
则D(0,0,0),P(0,0,1),B(λ,1,0),C(0,1,0), ![]() =(λ1,﹣1),点E是PC的中点,所以E(0,
=(λ1,﹣1),点E是PC的中点,所以E(0, ![]() ,
, ![]() ),
), ![]() =(0,
=(0, ![]() ,
, ![]() ),
),
于是 ![]() =0,即PB⊥DE.
=0,即PB⊥DE.
又已知EF⊥PB,而ED∩EF=E,所以PB⊥平面DEF.
因 ![]() =(0,1,﹣1),
=(0,1,﹣1), ![]() =0,则DE⊥PC,所以DE⊥平面PBC.
=0,则DE⊥PC,所以DE⊥平面PBC.
由DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,
即四面体BDEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF,∠EFB,∠DFB
(2)解法1:如图1,
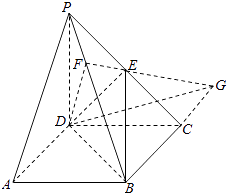
在面BPC内,延长BC与FE交于点G,则DG是平面DEF与平面ACBD的交线.
由(1)知,PB⊥平面DEF,所以PB⊥DG.
又因为PD⊥底面ABCD,所以PD⊥DG.而PD∩PB=P,所以DG⊥平面PBD.
所以DG⊥DF,DG⊥DB
故∠BDF是面DEF与面ABCD所成二面角的平面角,
设PD=DC=1,BC=λ,有BD= ![]() ,
,
在Rt△PDB中,由DF⊥PB,得∠DPB=∠FDB= ![]() ,
,
则 tan ![]() =tan∠DPF=
=tan∠DPF= ![]() =
= ![]() =
= ![]() ,解得
,解得 ![]() .
.
所以 ![]() =
= ![]() =
= ![]()
故当面DEF与面ABCD所成二面角的大小为 ![]() 时,
时, ![]() =
= ![]()
解法2:
由PD⊥底面ABCD,所以 ![]() =(0,0,1)是平面ACDB的一个法向量;
=(0,0,1)是平面ACDB的一个法向量;
由(1)知,PB⊥平面DEF,所以 ![]() =(﹣λ,﹣1,1)是平面DEF的一个法向量.
=(﹣λ,﹣1,1)是平面DEF的一个法向量.
若面DEF与面ABCD所成二面角的大小为 ![]() ,
,
则运用向量的数量积求解得出cos ![]() =
= ![]() =
= ![]() ,
,
解得 ![]() .所以所以
.所以所以 ![]() =
= ![]() =
= ![]()
故当面DEF与面ABCD所成二面角的大小为 ![]() 时,
时, ![]() =
= ![]()
【解析】(1)解法1:直线与直线,直线与平面的垂直的转化证明得出PB⊥EF,DE∩FE=E,所以PB⊥平面DEF,即可判断DE⊥平面PBC,PB⊥平面DEF,可知四面体BDEF的四个面都是直角三角形,确定直角. 解法2:以D为原点,射线DA,DC,DP分别为x,y,z轴的正半轴,建立空间直角坐标系,运用向量的数量积判断即可.
(2.)根据公理2得出DG是平面DEF与平面ACBD的交线.利用直线平面的垂直判断出DG⊥DF,DG⊥DB,根据平面角的定义得出∠BDF是面DEF与面ABCD所成二面角的平面角,转化到直角三角形求解即可.解法2:由PD⊥底面ABCD,所以 ![]() =(0,0,1)是平面ACDB的一个法向量;由(1)知,PB⊥平面DEF,所以
=(0,0,1)是平面ACDB的一个法向量;由(1)知,PB⊥平面DEF,所以 ![]() =(﹣λ,﹣1,1)是平面DEF的一个法向量.根据数量积得出夹角的余弦即可得出所求解的答案.
=(﹣λ,﹣1,1)是平面DEF的一个法向量.根据数量积得出夹角的余弦即可得出所求解的答案.


科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),当x≥0时,f(x)= ![]() ,则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
,则关于x的函数F(x)=f(x)﹣a(0<a<1)的所有零点之和为( )
A.3a﹣1
B.1﹣3a
C.3﹣a﹣1
D.1﹣3﹣a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 上的一个最高点的坐标为
上的一个最高点的坐标为![]() ,由此点到相邻最低点间的曲线与x轴交于点
,由此点到相邻最低点间的曲线与x轴交于点![]() ,若
,若![]() .
.
(1)求![]() 的解析式.
的解析式.
(2)求![]() 在
在![]() 上的值域.
上的值域.
(3)若对任意实数![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数a>0,函数f(x)=ln(1+ax)﹣ ![]() .
.
(Ⅰ)讨论f(x)在区间(0,+∞)上的单调性;
(Ⅱ)若f(x)存在两个极值点x1 , x2 , 且f(x1)+f(x2)>0,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b∈R,函数 ![]() ,g(x)=ex(e为自然对数的底数),且函数f(x)的图象与函数g(x)的图象在x=0处有公共的切线.
,g(x)=ex(e为自然对数的底数),且函数f(x)的图象与函数g(x)的图象在x=0处有公共的切线.
(Ⅰ)求b的值;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)若g(x)>f(x)在区间(﹣∞,0)内恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+3x2+1,若至少存在两个实数m,使得f(﹣m),f(1)、f(m+2)成等差数列,则过坐标原点作曲线y=f(x)的切线可以作( )
A.3条
B.2条
C.1条
D.0条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com