
【题目】设a,b∈R,函数 ![]() ,g(x)=ex(e为自然对数的底数),且函数f(x)的图象与函数g(x)的图象在x=0处有公共的切线.
,g(x)=ex(e为自然对数的底数),且函数f(x)的图象与函数g(x)的图象在x=0处有公共的切线.
(Ⅰ)求b的值;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)若g(x)>f(x)在区间(﹣∞,0)内恒成立,求a的取值范围.
【答案】(Ⅰ)f'(x)=x2+2ax+b,g'(x)=ex ,
由f'(0)=b=g'(0)=1,得b=1.
(Ⅱ)f'(x)=x2+2ax+1=(x+a)2+1﹣a2 ,
当a2≤1时,即﹣1≤a≤1时,f'(x)≥0,从而函数f(x)在定义域内单调递增,
当a2>1时, ![]() ,此时
,此时
若 ![]() ,f'(x)>0,则函数f(x)单调递增;
,f'(x)>0,则函数f(x)单调递增;
若 ![]() ,f'(x)<0,则函数f(x)单调递减;
,f'(x)<0,则函数f(x)单调递减;
若 ![]() 时,f'(x)>0,则函数f(x)单调递增.
时,f'(x)>0,则函数f(x)单调递增.
(Ⅲ)令h(x)=g'(x)﹣f'(x)=ex﹣x2﹣2ax﹣1,则h(0)=e0﹣1=0.h'(x)=ex﹣2x﹣2a,令u(x)=h'(x)=ex﹣2x﹣2a,则u'(x)=ex﹣2.
当x≤0时,u'(x)<0,从而h'(x)单调递减,
令u(0)=h'(0)=1﹣2a=0,得 ![]() .
.
先考虑 ![]() 的情况,此时,h'(0)=u(0)≥0;
的情况,此时,h'(0)=u(0)≥0;
又当x∈(﹣∞,0)时,h'(x)单调递减,所以h'(x)>0;
故当x∈(﹣∞,0)时,h(x)单调递增;
又因为h(0)=0,故当x<0时,h(x)<0,
从而函数g(x)﹣f(x)在区间(﹣∞,0)内单调递减;
又因为g(0)﹣f(0)=0,所以g(x)>f(x)在区间(﹣∞,0)恒成立.
接下来考虑 ![]() 的情况,此时,h'(0)<0,
的情况,此时,h'(0)<0,
令x=﹣a,则h'(﹣a)=e﹣a>0.
由零点存在定理,存在x0∈(﹣a,0)使得h'(x0)=0,
当x∈(x0 , 0)时,由h'(x)单调递减可知h'(x)<0,所以h(x)单调递减,
又因为h(0)=0,故当x∈(x0 , 0)时h(x)>0.
从而函数g(x)﹣f(x)在区间(x0 , 0)单调递增;
又因为g(0)﹣f(0)=0,所以当x∈(x0 , 0),g(x)<f(x).
综上所述,若g(x)>f(x)在区间(﹣∞,0)恒成立,则a的取值范围是 ![]()
【解析】(Ⅰ)求出两个函数的导数,利用函数f(x)的图象与函数g(x)的图象在x=0处有公共的切线.列出方程即可求解b.
(Ⅱ)求出导函数f'(x)=,通过﹣1≤a≤1时,当a2>1时,分别判断导函数的符号,推出函数的单调区间.
(Ⅲ)令h(x)=g'(x)﹣f'(x)=ex﹣x2﹣2ax﹣1,可得h(0)0.求出h'(x)=ex﹣2x﹣2a,令u(x)=h'(x)=ex﹣2x﹣2a,求出导数u'(x)=ex﹣2.当x≤0时,u'(x)<0,从而h'(x)单调递减,求出 ![]() .考虑
.考虑 ![]() 的情况,
的情况, ![]() 的情况,分别通过函数的单调性以及函数的最值,推出a的范围即可.
的情况,分别通过函数的单调性以及函数的最值,推出a的范围即可.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】某化工厂拟建一个下部为圆柱,上部为半球的容器(如图圆柱高为 ![]() ,半径为
,半径为 ![]() ,不计厚度,单位:米),按计划容积为
,不计厚度,单位:米),按计划容积为 ![]() 立方米,且
立方米,且 ![]() ,假设建造费用仅与表面积有关(圆柱底部不计 ),已知圆柱部分每平方米的费用为2千元,半球部分每平方米的费用为2千元,设该容器的建造费用为y千元.
,假设建造费用仅与表面积有关(圆柱底部不计 ),已知圆柱部分每平方米的费用为2千元,半球部分每平方米的费用为2千元,设该容器的建造费用为y千元.
(1)求y关于r的函数关系,并求其定义域;
(2)求建造费用最小时的 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在著名的汉诺塔问题中有三根针和套在一根针上的若干金属片,按下列规则,把金属片从一根针上全部移到另一根针上:①每次只能移动一个金属片;②在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.将n个金属片从1号针移到3号针最少需要移动的次数记为f(n),则f(6)=( ) 
A.31
B.33
C.63
D.65
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接DE,DF,BD,BE. 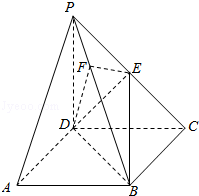
(1)证明:PB⊥平面DEF.试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(2)若面DEF与面ABCD所成二面角的大小为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量a=![]() cosωx+1,2sinωx,b=
cosωx+1,2sinωx,b=![]() cosωx-
cosωx-![]() ,cosωx), ω>0.
,cosωx), ω>0.
(Ⅰ)当ωx≠kπ+![]() ,k∈Z时,若向量c=(1,0),d=(
,k∈Z时,若向量c=(1,0),d=(![]() ,0),且(a-c)∥(b+d),求4sin2ωx-cos2ωx的值;
,0),且(a-c)∥(b+d),求4sin2ωx-cos2ωx的值;
(Ⅱ)若函数f(x)=a·b的图象的相邻两对称轴之间的距离为![]() ,当x∈[
,当x∈[![]() ],g时,求函数f(x)的单调递增区间.
],g时,求函数f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,所得图像对应的函数( )
个单位长度,所得图像对应的函数( )
A. 在区间![]() 上单调递减 B. 在区间
上单调递减 B. 在区间![]() 上单调递增
上单调递增
C. 在区间![]() 上单调递减 D. 在区间
上单调递减 D. 在区间![]() 上单调递增
上单调递增
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com