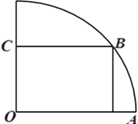
【题目】如图，在半径为3的圆形（为圆心）铝皮上截取一块矩形材料，其中点在圆弧上，点在两半径上，现将此矩形铝皮卷成一个以为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设矩形的边长，圆柱的体积为.

（1）写出体积关于的函数关系式，并指出定义域；

（2）当为何值时，才能使做出的圆柱形罐子体积最大？最大体积是多少？（圆柱体积公式： ， 为圆柱的底面积， 为圆柱的高）

【题目】在平面直角坐标系中，已知圆的方程为： ，直线的方程为．

（）当时，求直线被圆截得的弦长；

（）当直线被圆截得的弦长最短时，求直线的方程；

（）在（）的前提下，若为直线上的动点，且圆上存在两个不同的点到点的距离为，求点的横坐标的取值范围．

【题目】已知函数.

（1）求函数的最小正周期与单调递减区间；

（2）若函数的图象上的所有点的横坐标伸长到原来的倍，所得的图象与直线交点的横坐标由小到大依次是，求的值．

【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了至月份每月号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：

该兴趣小组确定的研究方案是：先从这六组数据中选取组，用剩下的组数据求线性回归方程，再用被选取的组数据进行检验.

（1）求选取的组数据恰好是相邻两月的概率；

（2）若选取的是1月与月的两组数据，请根据2至5月份的数据，求出关于的线性回归方程；

（3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过人，则认为得到的线性回归方程是理想的，试问该小组所得线性回归方程是否理想？

参考数据，

（参考公式： ，）

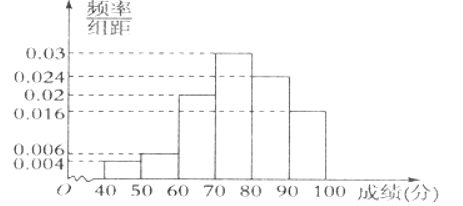
根据以上频率分布直方图，回答下列问题：

（1）求这100名学生成绩的及格率；（大于等于60分为及格）

（2）试比较这100名学生的平均成绩和中位数的大小.（精确到0.1）

【题目】已知，命题椭圆C1： 表示的是焦点在轴上的椭圆，命题对，直线与椭圆C2： 恒有公共点.

（1）若命题“”是假命题，命题“”是真命题，求实数的取值范围.

（2）若真假时，求椭圆C1、椭圆C2的上焦点之间的距离d的范围。

【题目】已知是定义在上的奇函数，且，若，时，有.

（1）证明在上是增函数；

（2）解不等式；

（3）若对，恒成立，求实数的取值范围.

某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿场售价与上市时间的关系用图一的一条折线表示；西红柿的种植成本与上市时间的关系用图二的抛物线段表示。

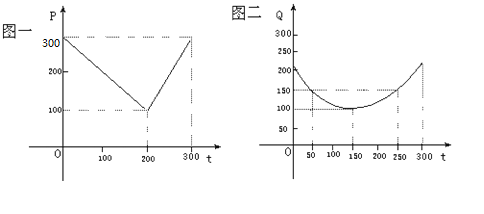
（Ⅰ）写出图一表示的市场售价与时间的函数关系式；写出图二表示的种植成本与上市时间的函数关系式；

（Ⅱ）假如设定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？（注：市场售价和种植成本的单位：元/102㎏，时间单位：天）

【题目】在直角坐标系xOy中，曲线 ，曲线C2的参数方程为： ，（θ为参数），以O为极点，x轴的正半轴为极轴的极坐标系．
（1）求C1 ， C2的极坐标方程；
（2）射线 与C1的异于原点的交点为A，与C2的交点为B，求|AB|．

【题目】已知二次函数满足，且．

（）求的解析式．

（）若函数在区间上是单调函数，求实数的取值范围．

（）若关于的方程有区间上有唯一实数根，求实数的取值范围（相等的实数根算一个）．