
科目: 来源: 题型:
【题目】在三棱锥ABCD中,BC⊥CD,Rt△BCD斜边上的高为1,三棱锥ABCD的外接球的直径是AB,若该外接球的表面积为16π,则三棱锥ABCD体积的最大值为( )
A.![]()
B.![]()
C.1
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C: ![]() =1(a>b>0)过点P(1,
=1(a>b>0)过点P(1, ![]() ).离心率为
).离心率为![]() .
.
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A,B两点.
①若直线l过椭圆C的右焦点,记△ABP三条边所在直线的斜率的乘积为t.
求t的最大值;
②若直线l的斜率为![]() ,试探究OA2+ OB2是否为定值,若是定值,则求出此
,试探究OA2+ OB2是否为定值,若是定值,则求出此
定值;若不是定值,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
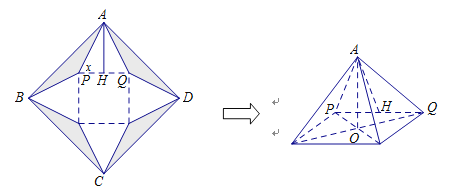
【题目】如图:设一正方形纸片ABCD边长为2分米,切去阴影部分所示的四个全等的等腰三角形,剩余为一个正方形和四个全等的等腰三角形,沿虚线折起,恰好能做成一个正四棱锥(粘接损耗不计),图中![]() ,O为正四棱锥底面中心.
,O为正四棱锥底面中心.
(Ⅰ)若正四棱锥的棱长都相等,求这个正四棱锥的体积V;
(Ⅱ)设等腰三角形APQ的底角为x,试把正四棱锥的侧面积S表示为x的函数,并求S的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一,秦九韶利用其多项式算法,给出了求高次代数方程的完整算法,这一成就比西方同样的算法早五六百年,如图是该算法求函数f(x)=x3+x+1零点的程序框图,若输入x=﹣1,c=1,d=0.1,则输出的x的值为( )
A.﹣0.6
B.﹣0.69
C.﹣0.7
D.﹣0.71
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x-1+![]() x2-2,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
x2-2,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
查看答案和解析>>
科目: 来源: 题型:
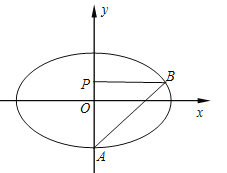
【题目】如图,点![]() 是椭圆
是椭圆![]() :
:![]() 的短轴位于
的短轴位于![]() 轴下方的端点,过
轴下方的端点,过![]() 作斜率为1的直线交椭圆于
作斜率为1的直线交椭圆于![]() 点,点
点,点![]() 在
在![]() 轴上,且
轴上,且![]() 轴,
轴, ![]() .
.
(1)若点![]() 的坐标为
的坐标为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)若点![]() 的坐标为
的坐标为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=sin2x+sinx+cosx,以下说法中不正确的是( )
A.f(x)周期为2π
B.f(x)最小值为﹣ ![]()
C.f(x)在区间[0, ![]() ]单调递增
]单调递增
D.f(x)关于点x= ![]() 对称
对称
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆M的圆心在直线![]() 上,且经过点A(-3,0),B(1,2).
上,且经过点A(-3,0),B(1,2).
(1)求圆M的方程;
(2)直线![]() 与圆M相切,且
与圆M相切,且![]() 在y轴上的截距是
在y轴上的截距是![]() 在x轴上截距的两倍,求直线
在x轴上截距的两倍,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
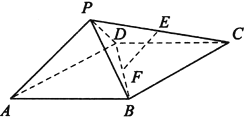
【题目】如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,
∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD;
(3)求四棱锥P—ABCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com