
科目: 来源: 题型:
【题目】已知函数f(x)=a-![]() -lnx,g(x)=ex-ex+1.
-lnx,g(x)=ex-ex+1.
(1)若a=2,求函数f(x)在点(1,f(1))处的切线方程;
(2)若f(x)=0恰有一个解,求a的值;
(3)若g(x)≥f(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】[选项4-4:坐标系与参数方程]
在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.
(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;
(2)直线l的参数方程是 ![]() (t为参数),l与C交与A,B两点,|AB|=
(t为参数),l与C交与A,B两点,|AB|= ![]() ,求l的斜率.
,求l的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个函数f(x),如果对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“保三角形函数”.
(1)判断f1(x)=x,f2(x)=log2(6+2sinx-cos2x)中,哪些是“保三角形函数”,哪些不是,并说明理由;
(2)若函数g(x)=lnx(x∈[M,+∞))是“保三角形函数”,求M的最小值;
(3)若函数h(x)=sinx(x∈(0,A))是“保三角形函数”,求A的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知A是椭圆E: ![]() =1的左顶点,斜率为k(k>0)的直线交E与A,M两点,点N在E上,MA⊥NA.
=1的左顶点,斜率为k(k>0)的直线交E与A,M两点,点N在E上,MA⊥NA.
(1)当|AM|=|AN|时,求△AMN的面积
(2)当2|AM|=|AN|时,证明: ![]() <k<2.
<k<2.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=(x+1)lnx﹣a(x﹣1).
(1)当a=4时,求曲线y=f(x)在(1,f(1))处的切线方程;
(2)若当x∈(1,+∞)时,f(x)>0,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点P(0,-2),椭圆E: ![]() 的离心率为
的离心率为![]() ,F是椭圆E的右焦点,直线PF的斜率为2,O为坐标原点.
,F是椭圆E的右焦点,直线PF的斜率为2,O为坐标原点.
(1)求椭圆E的方程;
(2)直线l被圆O:x2+y2=3截得的弦长为3,且与椭圆E交于A、B两点,求△AOB面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】借助计算机(器)作某些分段函数图象时,分段函数的表示有时可以利用函数![]() ,例如要表示分段函数g(x)=
,例如要表示分段函数g(x)=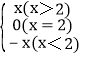 总可以将g(x)表示为g(x)=xh(x-2)+(-x)h(2-x).
总可以将g(x)表示为g(x)=xh(x-2)+(-x)h(2-x).
(1)设f(x)=(x2-2x+3)h(x-1)+(1-x2)h(1-x),请把函数f(x)写成分段函数的形式;
(2)已知G(x)=[(3a-1)x+4a]h(1-x)+logaxh(x-1)是R上的减函数,求a的取值范围;
(3)设F(x)=(x2+x-a+1)h(x-a)+(x2-x+a+1)h(a-x),求函数F(x)的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.
(1)证明:AC⊥HD′;
(2)若AB=5,AC=6,AE= ![]() ,OD′=2
,OD′=2 ![]() ,求五棱锥D′﹣ABCFE体积.
,求五棱锥D′﹣ABCFE体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】正方体ABCD-A1B1C1D1中,E为AB中点,F为CD1中点.

(1)求证:EF∥平面ADD1A1;
(2)求直线EF和平面CDD1C1所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com