
科目: 来源: 题型:
【题目】已知双曲线E:![]() ﹣
﹣![]() =1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
(1)求双曲线E的离心率;
(2)如图,O为坐标原点,动直线l分别交直线l1 , l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() ,点P(2,0).
,点P(2,0).
(I)求椭圆C的短轴长与离心率;
( II)过(1,0)的直线![]() 与椭圆C相交于M、N两点,设MN的中点为T,判断|TP|与|TM|的大小,并证明你的结论.
与椭圆C相交于M、N两点,设MN的中点为T,判断|TP|与|TM|的大小,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求:
①顾客所获的奖励额为60元的概率;
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和50元的两种球组成,或标有面值20元和40元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.
(I)求证:PB∥平面FAC;
(II)求三棱锥P-EAD的体积;
(III)求证:平面EAD⊥平面FAC.

查看答案和解析>>
科目: 来源: 题型:
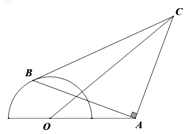
【题目】如图,半圆O的直径为2,A为直径延长线上一点,OA=2,B为半圆上任意一点,以线段AB为腰作等腰直角△ABC(C、O两点在直线AB的两侧),当∠AOB变化时,OC≤m恒成立,则m的最小值为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设F为抛物线![]() 的焦点,A、B是抛物线C上的两个动点,O为坐标原点.
的焦点,A、B是抛物线C上的两个动点,O为坐标原点.
(I)若直线AB经过焦点F,且斜率为2,求线段AB的长度|AB|;
(II)当OA⊥OB时,求证:直线AB经过定点M(4,0).
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在区间[a,b]上的连续函数y=f(x),如果![]() ,使得
,使得![]() ,则称
,则称![]() 为区间[a,b]上的“中值点”,下列函数:
为区间[a,b]上的“中值点”,下列函数:
①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() 中,在区间[O,1]上“中值点”多于一个的函数序号为( )
中,在区间[O,1]上“中值点”多于一个的函数序号为( )
A. ①② B. ①③ C. ②③ D. ①④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() 为其左、右顶点,
为其左、右顶点,![]() 为椭圆上除
为椭圆上除![]() ,
,![]() 外任意一点,若记直线
外任意一点,若记直线![]() ,
,![]() 斜率分别为
斜率分别为![]() ,
,![]() .
.
(1)求证:![]() 为定值;
为定值;
(2)若椭圆![]() 的长轴长为4,过点
的长轴长为4,过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,若
,若![]() 恰好为
恰好为![]() 与椭圆相交的弦的中点,求
与椭圆相交的弦的中点,求![]() 与椭圆相交的弦的中点的横坐标.
与椭圆相交的弦的中点的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com