【题目】已知关于直线对称，且圆心在轴上.

（1）求的标准方程；

（2）已经动点在直线上，过点引的两条切线、，切点分别为.

①记四边形的面积为，求的最小值；

②证明直线恒过定点.

【题目】已知函数.

（1）当时，求在区间上的最值；

（2）讨论函数的单调性；

（3）当时，有恒成立，求的取值范围.

【题目】建设生态文明，是关系人民福祉，关乎民族未来的长远大计.某市通宵营业的大型商场，为响应节能减排的号召，在气温超过时，才开放中央空调降温，否则关闭中央空调.如图是该市夏季一天的气温（单位：）随时间（，单位：小时）的大致变化曲线，若该曲线近似的满足函数关系.

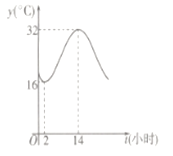
（1）求函数的表达式；

（2）请根据（1）的结论，判断该商场的中央空调应在本天内何时开启？何时关闭？

①函数是偶函数；

②当时，函数的值域是；

③若扇形的周长为，圆心角为，则该扇形的弧长为6 cm；

④已知定义域为的函数，当且仅当时，成立.

则上述结论中正确的是______（写出所有正确结论的序号）．

【题目】“圆材埋壁”是《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，学会一寸，锯道长一尺，问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知道大小，用锯取锯它，锯口深一寸，锯道长一尺，问这块圆柱形木材的直径是多少？现有圆柱形木材一部分埋在墙壁中，截面如图所示，已知弦尺，弓形高寸，则阴影部分面积约为（注：，，1尺=10寸）（ ）

A. 6.33平方寸B. 6.35平方寸

C. 6.37平方寸D. 6.39平方寸

【题目】位于潍坊滨海的“滨海之眼”摩天轮是世界上最高的无轴摩天轮，该摩天轮的直径均为124米，中间没有任何支撑，摩天轮顺时针匀速旋转一圈需要30分钟，当乘客乘坐摩天轮到达最高点时，距离地面145米，可以俯瞰白浪河全景，图中与地面垂直，垂足为点，某乘客从处进入处的观景舱，顺时针转动分钟后，第1次到达点，此时点与地面的距离为114米，则（ ）

A. 16分钟B. 18分钟C. 20分钟D. 22分钟

【题目】设为三角形的三边，求证：

【题目】已知椭圆C： （a＞b＞0）的两个焦点分别为F1（﹣1，0），F2（1，0），且椭圆C经过点 ．
（1）求椭圆C的离心率：
（2）设过点A（0，2）的直线l与椭圆C交于M，N两点，点Q是线段MN上的点，且 ，求点Q的轨迹方程．

【题目】已知幂函数满足．

（1）求函数的解析式；

（2）若函数，是否存在实数使得的最小值为0？若存在，求出的值；若不存在，说明理由；

（3）若函数，是否存在实数，使函数在上的值域为？若存在，求出实数的取值范围；若不存在，说明理由．

（参考数据：）

A. 12 B. 24 C. 48 D. 96