【题目】将函数f（x）=2cos2x的图象向右平移 个单位后得到函数g（x）的图象，若函数g（x）在区间[0， ]和[2a， ]上均单调递增，则实数a的取值范围是（ ）
A.[ ， ]
B.[ ， ]
C.[ ， ]
D.[ ， ]

经长期观测，y=f（t）的曲线可近似地看成是函数y=Acosωt＋b的图象．

（1）根据以上数据，求出函数y=Acosωt＋b的最小正周期T、振幅A及函数表达式；

（2）依据规定，当海浪高度高于1米时才对冲浪爱好者开放，请依据（1）的结论，判断一天内的上午8时到晚上20时之间，有多长时间可供冲浪者进行运动？

(1)当a=1时，求不等式f(x)≤1的解集；

(2)设关于x的不等式f(x)≤-2x+1的解集为P，且 P，求a的取值范围.

【题目】如图，在直三棱柱ABC﹣A1B1C1中，AB⊥AC，AB=AA1=2，AC= ，过BC的中点D作平面ACB1的垂线，交平面ACC1A1于E，则BE与平面ABB1A1所成角的正切值为（ ）
A.
B.
C.
D.

【题目】设点M（x1 ， f（x1））和点N（x2 ， g（x2））分别是函数f（x）=ex﹣ x2和g（x）=x﹣1图象上的点，且x1≥0，x2＞0，若直线MN∥x轴，则M，N两点间的距离的最小值为（ ）
A.1
B.2
C.3
D.4

(1)求证：AB⊥平面ADC；

(2)若AD＝1，AB＝，求点B到平面ADE的距离．

【题目】命题p：f(x)＝－x2＋2ax＋1－a在x∈[0,1]时的最大值不超过2，命题q：正数x，y满足x＋2y＝8，且 恒成立. 若p∨(q)为假命题，求实数a的取值范围．

(1)求函数f(x)的解析式；

(2)当x∈[0,3]时，求函数f(x)的值域．

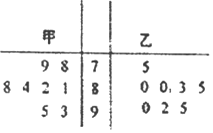
（1）现要从中选派一人参加数学竞赛，对预赛成绩的平均值和方差进行分析，你认为哪位学生的成绩更稳定？请说明理由；

（2）求在甲同学的8次预赛成绩中，从不小于80分的成绩中随机抽取2个成绩，列出所有结果，并求抽出的2个成绩均大于85分的概率．

A. MN∥AB B. MN与BC所成的角为45°

C. OC⊥平面VAC D. 平面VAC⊥平面VBC