【题目】已知数列的前项和为，满足，．数列满足，，且．

（1）求数列和的通项公式；

（2）若，数列的前项和为，对任意的，都有，求实数的取值范围；

（3）是否存在正整数，，使，，（）成等差数列，若存在，求出所有满足条件的，，若不存在，请说明理由．

A. 3 971B. 3 972C. 3 973D. 3 974

【题目】袋子中有四张卡片，分别写有“瓷、都、文、明”四个字，有放回地从中任取一张卡片，将三次抽取后“瓷”“都”两个字都取到记为事件，用随机模拟的方法估计事件发生的概率.利用电脑随机产生整数0，1，2，3四个随机数，分别代表“瓷、都、文、明”这四个字，以每三个随机数为一组，表示取卡片三次的结果，经随机模拟产生了以下18组随机数：

由此可以估计事件发生的概率为（ ）

A. B. C. D.

A. B. C. D.

【题目】甲、乙、丙三人玩抽红包游戏，现将装有5元、3元、2元的红包各3个，放入一不透明的暗箱中并搅拌均匀，供3人随机抽取． （Ⅰ）若甲随机从中抽取3个红包，求甲抽到的3个红包中装有的金额总数小于10元的概率．
（Ⅱ）若甲、乙、丙按下列规则抽取：
①每人每次只抽取一个红包，抽取后不放回；
②甲第一个抽取，甲抽完后乙再抽取，丙抽完后甲再抽取…，依次轮流；
③一旦有人抽到装有5元的红包，游戏立即结束．
求甲抽到的红包的个数X的分布列及数学期望．

【题目】在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若= + ，则+的最大值为__________．

【题目】已知函数f（x）＝ax2+bx+c（a≠0）满足f（0）＝0，对于任意x∈R，都有f（x）≥x，且，令g（x）＝f（x）﹣|λx﹣1|（λ＞0）．

（1）求函数f（x）的表达式；

（2）求函数g（x）的单调区间；

（3）当λ＞2时，判断函数g（x）在区间（0，1）上的零点个数，并说明理由．

【题目】如图所示的几何体ABCDE中，DA⊥平面EAB，CB∥DA，EA=DA=AB=2CB，EA⊥ AB，M是EC上的点（不与端点重合），F为DA上的点，N为BE的中点．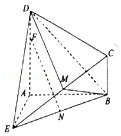

（Ⅰ）若M是EC的中点，AF=3FD，求证：FN∥平面MBD；
（Ⅱ）若平面MBD与平面ABD所成角（锐角）的余弦值为 ，试确定点M在EC上的位置．

【题目】已知△ABC的三个内角A，B，C的对边分别是a，b，c，若向量 =（a+c，sinB）， =（b﹣c，sinA﹣sinC），且 ∥ ． （Ⅰ）求角A的大小；
（Ⅱ）设函数f（x）=tanAsinωxcosωx﹣cosAcos2ωx（ω＞0），已知其图象的相邻两条对称轴间的距离为 ，现将y=f（x）的图象上各点向左平移 个单位，再将所得图象上各点的横坐标伸长为原来的2倍，得到函数y=g（x）的图象，求g（x）在[0，π]上的值域．

【题目】已知函数有唯一零点，则a=

A. B. C. D.