
科目: 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A.1盏
B.3盏
C.5盏
D.9盏
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,且圆心在直线
,且圆心在直线![]() :
:![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线与圆
的直线与圆![]() 交于
交于![]() 两点,问在直线
两点,问在直线![]() 上是否存在定点
上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,请求出点
恒成立?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C与A,B两点,圆M是以线段AB为直径的圆.
(Ⅰ)证明:坐标原点O在圆M上;
(Ⅱ)设圆M过点P(4,﹣2),求直线l与圆M的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 两地相距
两地相距![]() 千米,汽车从
千米,汽车从![]() 地匀速行驶到
地匀速行驶到![]() 地,速度不超过
地,速度不超过![]() 千米小时,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度
千米小时,已知汽车每小时的运输成本(单位:元)由可变部分和固定部分两部分组成:可变部分与速度![]() 的平方成正比,比例系数为
的平方成正比,比例系数为![]() ,固定部分为
,固定部分为![]() 元,
元,
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (千米小时)的函效:并求出当
(千米小时)的函效:并求出当![]() 时,汽车应以多大速度行驶,才能使得全程运输成本最小;
时,汽车应以多大速度行驶,才能使得全程运输成本最小;
(2)随着汽车的折旧,运输成本会发生一些变化,那么当![]() ,此时汽车的速度应调整为多大,才会使得运输成本最小,
,此时汽车的速度应调整为多大,才会使得运输成本最小,
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为确定下一年度投人某种产品的宣传费,需了解年宣传费![]() 对年销售额(单位:万元)的影响,对近6年的年宣传费
对年销售额(单位:万元)的影响,对近6年的年宣传费![]() 和年销售额
和年销售额![]() 数据进行了研究,发现宣传费
数据进行了研究,发现宣传费![]() 和年销售额
和年销售额![]() 具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.
具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.

(I)根据表中数据建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅱ)利用(I)中的回归方程预测该公司如果对该产品的宜传费支出为10万元时销售额是![]() 万元,该公司计划从10名中层管理人员中挑选3人担任总裁助理,10名中层管理人员中有2名是技术部骨干,记所挑选3人中技术部骨干人数为
万元,该公司计划从10名中层管理人员中挑选3人担任总裁助理,10名中层管理人员中有2名是技术部骨干,记所挑选3人中技术部骨干人数为![]() 且随机变量
且随机变量![]() ,求
,求![]() 的概率分布列与数学期望.
的概率分布列与数学期望.
附:回归直线的倾斜率截距的最小二乘估计公式分别为:
 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】随着![]() 业的迅速发展计算机也在迅速更新换代,平板电脑因使用和移动便捷以及时尚新潮性,而备受人们尤其是大学生的青睐,为了解大学生购买平板电脑进行学习的学习情况,某大学内进行了一次匿名调查,共收到1500份有效问卷.调查结果显示700名女学生中有300人,800名男生中有400人拥有平板电脑.
业的迅速发展计算机也在迅速更新换代,平板电脑因使用和移动便捷以及时尚新潮性,而备受人们尤其是大学生的青睐,为了解大学生购买平板电脑进行学习的学习情况,某大学内进行了一次匿名调查,共收到1500份有效问卷.调查结果显示700名女学生中有300人,800名男生中有400人拥有平板电脑.
(Ⅰ)完成下列列联表:
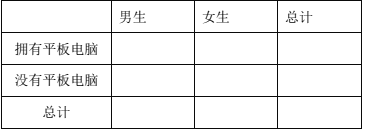
(Ⅱ)分析是否有![]() 的把握认为购买平板电脑与性别有关?
的把握认为购买平板电脑与性别有关?
附:独立性检验临界值表:

(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】校运动会高二理三个班级的3名同学报名参加铅球、跳高、三级跳远3个运动项目,每名同学都可以从3个运动项目中随机选择一个,且每个人的选择相互独立.
(1)求3名同学恰好选择了2个不同运动项目的概率;
(Ⅱ)设选择跳高的人数为![]() 试求
试求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0),四点P1(1,1),P2(0,1),P3(﹣1,
=1(a>b>0),四点P1(1,1),P2(0,1),P3(﹣1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.(12分)
)中恰有三点在椭圆C上.(12分)
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为﹣1,证明:l过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解学生暑假阅读名著的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.
|
|
|
|
| |
男生 |
|
|
|
|
|
女生 |
|
|
|
|
|
(![]() )从这班学生中任选一名男生,一名女生,求这两名学生阅读名著本数之和为
)从这班学生中任选一名男生,一名女生,求这两名学生阅读名著本数之和为![]() 的概率?
的概率?
(![]() )若从阅读名著不少于
)若从阅读名著不少于![]() 本的学生中任选
本的学生中任选![]() 人,设选到的男学生人数为
人,设选到的男学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
(![]() )试判断男学生阅读名著本数的方差
)试判断男学生阅读名著本数的方差![]() 与女学生阅读名著本数的方程
与女学生阅读名著本数的方程![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com