
科目: 来源: 题型:
【题目】已知数列{an},{bn}都是单调递增数列,若将这两个数列的项按由小到大的顺序排成一列(相同的项视为一项),则得到一个新数列{cn}.
(1)设数列{an},{bn}分别为等差、等比数列,若a1=b1=1,a2=b3 , a6=b5 , 求c20;
(2)设{an}的首项为1,各项为正整数,bn=3n , 若新数列{cn}是等差数列,求数列{cn} 的前n项和Sn;
(3)设bn=qn﹣1(q是不小于2的正整数),c1=b1 , 是否存在等差数列{an},使得对任意的n∈N* , 在bn与bn+1之间数列{an}的项数总是bn?若存在,请给出一个满足题意的等差数列{an};若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=xex﹣ax2(a∈R).
(1)若函数g(x)= ![]() 是奇函数,求实数a的值;
是奇函数,求实数a的值;
(2)若对任意的实数a,函数h(x)=kx+b(k,b为实常数)的图象与函数f(x)的图象总相切于一个定点. ①求k与b的值;
②对(0,+∞)上的任意实数x1 , x2 , 都有[f(x1)﹣h(x1)][f(x2)﹣h(x2)]>0,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂要制造A种电子装置45台,B种电子装置55台,需用薄钢板给每台装置配一个外壳,已知薄钢板的面积有两种规格:甲种薄钢板每张面积2m2,可做A、B的外壳分别为3个和5个,乙种薄钢板每张面积3m2,可做A、B的外壳分别为6个和6个,求两种薄钢板各用多少张,才能使总的面积最小.
查看答案和解析>>
科目: 来源: 题型:
【题目】某射手射击1次,击中目标的概率是0.9,他连续射击4次,且他各次射击是否击中目标相互之间没有影响.有下列结论:
①他第3次击中目标的概率是0.9; ②他恰好击中目标3次的概率是0.93×0.1;
③他至少击中目标1次的概率是1-0.14 ④他恰好有连续2次击中目标的概率为3×0.93×0.1
其中正确结论的序号是______
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分![]() 分)
分)
已知圆![]() ,过点
,过点![]() 作直线
作直线![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点.
两点.
(Ⅰ)当![]() 经过圆心
经过圆心![]() 时,求直线
时,求直线![]() 的方程.
的方程.
(Ⅱ)当直线![]() 的倾斜角为
的倾斜角为![]() 时,求弦
时,求弦![]() 的长.
的长.
(Ⅲ)求直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】在某互联网大会上,为了提升安全级别,将5名特警分配到3个重要路口执勤,每个人只能选择一个路口,每个路口最少1人,最多3人,且甲和乙不能安排在同一个路口,则不同的安排方法有( )
A. 180种 B. 150种 C. 96种 D. 114种
查看答案和解析>>
科目: 来源: 题型:
【题目】已知A、F分别是椭圆C: ![]() +
+ ![]() =1(a>b>0)的左顶点、右焦点,点P为椭圆C上一动点,当PF⊥x轴时,AF=2PF.
=1(a>b>0)的左顶点、右焦点,点P为椭圆C上一动点,当PF⊥x轴时,AF=2PF.
(1)求椭圆C的离心率;
(2)若椭圆C存在点Q,使得四边形AOPQ是平行四边形(点P在第一象限),求直线AP与OQ的斜率之积;
(3)记圆O:x2+y2= ![]() 为椭圆C的“关联圆”.若b=
为椭圆C的“关联圆”.若b= ![]() ,过点P作椭圆C的“关联圆”的两条切线,切点为M、N,直线MN的横、纵截距分别为m、n,求证:
,过点P作椭圆C的“关联圆”的两条切线,切点为M、N,直线MN的横、纵截距分别为m、n,求证: ![]() +
+ ![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100﹣80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮? 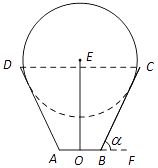
查看答案和解析>>
科目: 来源: 题型:
【题目】某市组织了一次高二调研考试,考试后统计的数学成绩服从正态分布,其密度函数![]() , x∈(-∞,+∞),则下列命题不正确的是( )
, x∈(-∞,+∞),则下列命题不正确的是( )
A. 该市这次考试的数学平均成绩为80分
B. 分数在120分以上的人数与分数在60分以下的人数相同
C. 分数在110分以上的人数与分数在50分以下的人数相同
D. 该市这次考试的数学成绩标准差为10
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 对一切实数
对一切实数![]() 都有
都有![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式,并用定义法证明
的解析式,并用定义法证明![]() 在
在![]() 单调递增;
单调递增;
(3)已知![]() ,设P:
,设P:![]() ,不等式
,不等式![]() 恒成立,Q:
恒成立,Q:![]() 时,
时,![]() 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的![]() 的集合记为A,满足Q成立的
的集合记为A,满足Q成立的![]() 集合记为B,求
集合记为B,求![]() (R为全集)。
(R为全集)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com