
科目: 来源: 题型:
【题目】首届中国国际进口博览会在2018年11月5日—10日在上海国家会展中心举办。会议期间,某公司欲采购东南亚某水果种植基地的水果,公司刘总经理与该种植基地的负责人陈老板商定一次性采购一种水果的采购价![]() (元/吨)与采购量
(元/吨)与采购量![]() (吨)之间的函数关系的图象如图中的折线
(吨)之间的函数关系的图象如图中的折线![]() 所示(不包含端点
所示(不包含端点![]() ,但包含端点
,但包含端点![]() ).
).
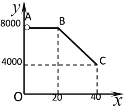
(Ⅰ)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(Ⅱ)已知该水果种植基地种植该水果的成本是2800元/吨,那么刘总经理的采购量为多少时,该水果基地在这次买卖中所获得利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线C1:x2=4y,C2:x2=﹣2py(p>0),点M(x0 , y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x0=1﹣ ![]() 时,切线MA的斜率为﹣
时,切线MA的斜率为﹣ ![]() .
. 
(1)求P的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为 ![]() .
.
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由;
(3)若点M的横坐标为 ![]() ,直线l:y=kx+
,直线l:y=kx+ ![]() 与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当
与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当 ![]() ≤k≤2时,|AB|2+|DE|2的最小值.
≤k≤2时,|AB|2+|DE|2的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四棱锥P - ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC![]()
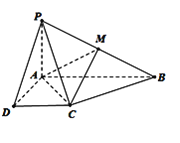
(1)证明平面PAD⊥平面PCD;
(2)求AC与PB所成角的余弦值;
(3)求平面AMC与平面BMC所成二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知三点O(0,0),A(﹣2,1),B(2,1),曲线C上任意一点M(x,y)满足| ![]() +
+ ![]() |=
|= ![]() (
( ![]() +
+ ![]() )+2.
)+2.
(1)求曲线C的方程;
(2)动点Q(x0 , y0)(﹣2<x0<2)在曲线C上,曲线C在点Q处的切线为直线l:是否存在定点P(0,t)(t<0),使得l与PA,PB都相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值.若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设椭圆 ![]() 的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
的左右顶点分别为A,B,点P在椭圆上且异于A,B两点,O为坐标原点.
(1)若直线AP与BP的斜率之积为 ![]() ,求椭圆的离心率;
,求椭圆的离心率;
(2)若|AP|=|OA|,证明直线OP的斜率k满足|k|> ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.05 |
第2组 | [60,70) |
| 0.35 |
第3组 | [70,80) | 30 |
|
第4组 | [80,90) | 20 | 0.20 |
第5组 | [90,100] | 10 | 0.10 |
合计 | 100 | 1.00 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com