
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 与
与![]() 轴交于
轴交于![]() 两点,且
两点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的一个动点,且直线
上的一个动点,且直线![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点.是否存在点
两点.是否存在点![]() 使得以
使得以![]() 为直径的圆经过点
为直径的圆经过点![]() ?若存在,求出点
?若存在,求出点![]() 的横坐标;若不存在,说明理由.
的横坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学的高二(1)班男同学有45名,女同学有15名,老师按照分层抽样的方法组建了一个4人的课外兴趣小组.
(1)求课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(3)试验结束后,第一次做试验的同学得到的试验数据为68,70,71,72,74,第二次做试验的同学得到的试验数据为69,70,70,72,74 ,请问哪位同学的实验更稳定?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题:
①对于任意一个圆O,其“优美函数“有无数个”;
②函数 ![]() 可以是某个圆的“优美函数”;
可以是某个圆的“优美函数”;
③正弦函数y=sinx可以同时是无数个圆的“优美函数”;
④函数y=f(x)是“优美函数”的充要条件为函数y=f(x)的图象是中心对称图形.
其中正确的命题是( )
A.①③
B.①③④
C.②③
D.①④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形![]() 为梯形,
为梯形,![]() 平面
平面![]() ,
,![]() ,
,
![]() 为
为![]() 中点.
中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,找出具体位置,并进行证明:若不存在,请分析说明理由.
?若存在,找出具体位置,并进行证明:若不存在,请分析说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】省农科站要检测某品牌种子的发芽率,计划采用随机数表法从该品牌![]() 粒种子中抽取
粒种子中抽取![]() 粒进行检测,现将这
粒进行检测,现将这![]() 粒种子编号如下
粒种子编号如下![]() ,
,![]() ,
,![]() ,
,![]() ,若从随机数表第
,若从随机数表第![]() 行第
行第![]() 列的数
列的数![]() 开始向右读,则所抽取的第
开始向右读,则所抽取的第![]() 粒种子的编号是 .(下表是随机数表第
粒种子的编号是 .(下表是随机数表第![]() 行至第
行至第![]() 行)
行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解本校学生在校小卖部的月消费情况,随机抽取了60名学生进行统计.得到如下样本频数分布表:
月消费金额(单位:元) |
|
|
|
|
|
|
人数 | 30 | 6 | 9 | 10 | 3 | 2 |
记月消费金额不低于300元为“高消费”,已知在样本中随机抽取1人,抽到是男生“高消费”的概率为![]() .
.
(1)从月消费金额不低于400元的学生中随机抽取2人,求至少有1人月消费金额不低于500元的概率;
(2)请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“高消费”与“男女性别”有关,说明理由.
的把握认为“高消费”与“男女性别”有关,说明理由.
高消费 | 非高消费 | 合计 | |
男生 | |||
女生 | 25 | ||
合计 | 60 |
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() ,其中)
,其中)
查看答案和解析>>
科目: 来源: 题型:
【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.
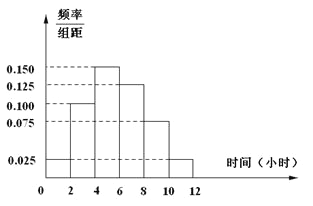
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有![]() 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:
![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知F2、F1是双曲线 ![]() =1(a>0,b>0)的上、下焦点,点F2关于渐近线的对称点恰好落在以F1为圆心,|OF1|为半径的圆上,则双曲线的离心率为( )
=1(a>0,b>0)的上、下焦点,点F2关于渐近线的对称点恰好落在以F1为圆心,|OF1|为半径的圆上,则双曲线的离心率为( )
A.3
B.![]()
C.2
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com