
科目: 来源: 题型:
【题目】某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知某学生选修甲而不选修乙和丙的概率为0.08,选修甲和乙而不选修丙的概率是0.12,至少选修一门的概率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率;
(2)求ξ的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC中,a,b,c分别是角A、B、C的对边,向量 ![]() =(2sinB,2﹣cos2B),
=(2sinB,2﹣cos2B), ![]() =(2sin2(
=(2sin2( ![]() +
+ ![]() ),﹣1)且
),﹣1)且 ![]() ⊥
⊥ ![]() .
.
(1)求角B的大小;
(2)若a= ![]() ,b=1,求c的值.
,b=1,求c的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是 . (写出所有正确说法的序号)
①若p是q的充分不必要条件,则p是q的必要不充分条件;
②命题“x∈R,x2+1>3x”的否定是“x∈R,x2+1<3x”;
③设x,y∈R.命题“若xy=0,则x2+y2=0”的否命题是真命题;
④若 ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】若n是一个三位正整数,且n的个位数字大于十位数字,十位数字大于百位数字,则称n为“三位递增数”(如137,359,567等).
在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得-1分;若能被10整除,得1分.
(1)写出所有个位数字是5的“三位递增数”;
(2)若甲参加活动,求甲得分X的分布列和数学期望E(X).
查看答案和解析>>
科目: 来源: 题型:
【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
| 优秀 | 非优秀 | 总计 |
甲班 | 10 | ||
乙班 | 30 | ||
总计 | 105 |
已知在全部105人中随机抽取1人为优秀的概率为![]() .
.
(1)请完成上面的列联表;(把列联表自己画到答题卡上)
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”?
参考公式:![]()
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两个小组各10名学生的英语口语测试成绩如下(单位:分).
甲组:76,90,84,86,81,87,86,82,85,83 乙组:82,84,85,89,79,80,91,89,79,74
现从这20名学生中随机抽取一人,将“抽出的学生为甲组学生”记为事件A;“抽出学生的英语口语测试成绩不低于85分”记为事件B,则P(AB)、P(A|B)的值分别是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】始于2007年初的美国次贷危机,至2008年中期,已经演变为全球金融危机.受此影响,国际原油价格从2008年7月每桶最高的147美元开始大幅下跌,9月跌至每桶97美元.你能求出国际原油价格7月到9月之间平均每月下降的百分比吗?若按此计算,到什么时间跌至谷底(即每桶34美元)?
查看答案和解析>>
科目: 来源: 题型:
【题目】某地为了了解地区100000户家庭的用电情况,采用分层抽样的方法抽取了500户家庭的月均用电量,并根据这500户家庭的月均用电量画出频率分布直方图(如图),则该地区100000户家庭中月均用电度数在[70,80]的家庭大约有户. 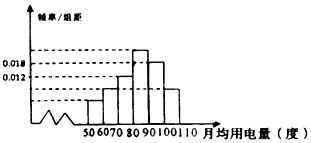
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,圆C的普通方程为![]() 在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为![]() .
.![]() Ⅰ
Ⅰ![]() 写出圆C的参数方程和直线l的直角坐标方程;
写出圆C的参数方程和直线l的直角坐标方程;![]() Ⅱ
Ⅱ![]() 设直线l与x轴和y轴的交点分别为A、B,P为圆C上的任意一点,求
设直线l与x轴和y轴的交点分别为A、B,P为圆C上的任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 为等边三角形,且平面
为等边三角形,且平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)证明: ![]() ;
;
(Ⅱ)若棱锥![]() 的体积为
的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】【试题分析】(I) 取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .利用等腰三角形的性质和矩形的性质可证得
.利用等腰三角形的性质和矩形的性质可证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,故
,故![]() ,故
,故![]() .(II) 可知
.(II) 可知![]() 是棱锥的高,利用体积公式求得
是棱锥的高,利用体积公式求得![]() ,利用勾股定理和等腰三角形的性质求得
,利用勾股定理和等腰三角形的性质求得![]() 的值,进而求得面积.
的值,进而求得面积.
【试题解析】
证明:(Ⅰ)取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() ,
,
∵![]() 为等边三角形,∴
为等边三角形,∴![]() .
.
底面![]() 中,可得四边形
中,可得四边形![]() 为矩形,∴
为矩形,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,所以
,所以![]() .
.
(Ⅱ)由面![]() 面
面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,所以
,所以![]() 为棱锥
为棱锥![]() 的高,
的高,
由![]() ,知
,知![]() ,
,
![]()
![]()
![]() ,
,
∴![]() .
.
由(Ⅰ)知![]() ,
,![]() ,∴
,∴![]() .
.
![]() .
.
由![]() ,可知
,可知![]() 平面
平面![]() ,∴
,∴![]() ,
,
因此![]() .
.
在![]() 中
中![]() ,
,![]() ,
,
取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() ,
,![]() ,
,
∴![]()
![]() .
.
所以棱锥![]() 的侧面积为
的侧面积为![]() .
.
【题型】解答题
【结束】
20
【题目】已知圆![]() 经过椭圆
经过椭圆![]() :
: ![]() 的两个焦点和两个顶点,点
的两个焦点和两个顶点,点![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 上的两点,它们在
上的两点,它们在![]() 轴两侧,且
轴两侧,且![]() 的平分线在
的平分线在![]() 轴上,
轴上, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)证明:直线![]() 过定点.
过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com