【题目】已知各项均不为0的数列{an}满足a1=a，a2=b，且an2=an﹣1an+1+λ（n≥2，n∈N），其中λ∈R．
（1）若λ=0，求证：数列{an}是等比数列；
（2）求证：数列{an}是等差数列的充要条件是λ=（b﹣a）2；
（3）若数列{bn}为各项均为正数的等比数列，且对任意的n∈N* ， 满足bn﹣an=1，求证：数列{（﹣1）nanbn}的前2n项和为常数．

【题目】如图，在平面直角坐标系xOy中，椭圆C： =1（a＞1）的左、右顶点分别为A、B，P是椭圆C上任一点，且点P位于第一象限．直线PA交y轴于点Q，直线PB交y轴于点R．当点Q坐标为（0，1）时，点R坐标为（0，2）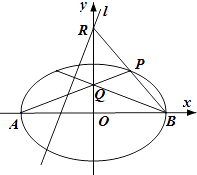

（1）求椭圆C的标准方程；
（2）求证： 为定值；
（3）求证：过点R且与直线QB垂直的直线经过定点，并求出该定点的坐标．

①复数z在复平面内的对应点位于第二象限；

②z·＋2iz＝8＋ai(a∈R)．

求a的取值范围．

【题目】如图，江的两岸可近似的看成两平行的直线，江岸的一侧有A，B两个蔬菜基地，江的另一侧点C处有一个超市．已知A、B、C中任意两点间的距离为20千米．超市欲在AB之间建一个运输中转站D，A，B两处的蔬菜运抵D处后，再统一经过货轮运抵C处．由于A，B两处蔬菜的差异，这两处的运输费用也不同．如果从A处出发的运输费为每千米2元，从B处出发的运输费为每千米1元，货轮的运输费为每千米3元．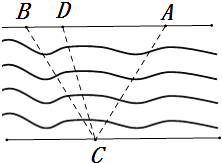

（1）设∠ADC=α，试将运输总费用S（单位：元）表示为α的函数S（α），并写出自变量的取值范围；
（2）问中转站D建在何处时，运输总费用S最小？并求出最小值．

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是正方形．点E是棱PC的中点，平面ABE与棱PD交于点F．
（Ⅰ）求证：AB∥EF；
（Ⅱ）若PA=AD，且平面PAD⊥平面ABCD，求证：AF⊥平面PCD．

tan 30°＋tan 30°＋tan 120°＝tan 30°·tan 30°·tan 120°，

tan 60°＋tan 60°＋tan 60°＝tan 60°·tan 60°·tan 60°，

tan 30°＋tan 45°＋tan 105°＝tan 30°·tan 45°·tan 105°.

分析上述各式的共同特点，猜想出表示的一般规律，并加以证明．

A. 以原点为圆心，以2为半径的圆

B. 两个点，其坐标为(2，2)，(－2，－2)

C. 以原点为圆心，以2为半径的圆和过原点的一条直线

D. 以原点为圆心，以2为半径的圆，并且除去两点(，)，(－，－)

【题目】在△ABC中，角A、B、C的对边分别为a、b、c（a＜b＜c）．已知向量 =（a，c）， =（cosC，cosA）满足 = （a+c）．
（1）求证：a+c=2b；
（2）若2csinA﹣ a=0，且c﹣a=8，求△ABC的面积S．

A. “x<1”是“log2(x+1)<1”的充分不必要条件

B. 命题“x>0，2x>1”的否定是“x0≤0，≤1”

C. 命题“若a≤b，则ac2≤bc2”的逆命题是真命题

D. 命题“若a+b≠5，则a≠2或b≠3”的逆否命题为真命题

【题目】在△ABC中，角A、B、C的对边分别为a、b、c（a＜b＜c）．已知向量 =（a，c）， =（cosC，cosA）满足 = （a+c）．
（1）求证：a+c=2b；
（2）若2csinA﹣ a=0，且c﹣a=8，求△ABC的面积S．