
科目: 来源: 题型:
【题目】若lg(3x)+lg y=lg(x+y+1),则xy的最小值为( )
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】
先根据对称的运算性质化简得到3xy=x+y+1,再根据基本不等式即可求出答案.
∵lg(3x)+lgy=lg(3xy)=lg(x+y+1),x>0,y>0,
∴3xy=x+y+1,
∴3xy≥3![]() ,当且仅当x=y=1时取等号,
,当且仅当x=y=1时取等号,
即xy≥1,
∴xy的最小值是1,
故选:A
【点睛】
在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误
【题型】单选题
【结束】
12
【题目】已知两定点![]() ,如果动点
,如果动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹所包围的图形的面积等于( )
的轨迹所包围的图形的面积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】等比数列{an}是递减数列,前n项的积为Tn,若T13=4T9,则a8a15=( )
A. 2 B. ±2 C. 4 D. ±4
【答案】A
【解析】
由题意可得 q>1,且 an >0,由条件可得 a1a2…a13=4a1a2…a9,化简得a10a11a12a13=4,再由 a8a15=a10a13=a11a12,求得a8a15的值.
等比数列{an}是递增数列,其前n项的积为Tn(n∈N*),若T13=4T9 ,设公比为q,
则由题意可得 q>1,且 an >0.
∴a1a2…a13=4a1a2…a9,∴a10a11a12a13=4.
又由等比数列的性质可得 a8a15=a10a13=a11a12,∴a8a15=2.
故选:A.
【点睛】
本题主要考查等比数列的定义和性质,求得 a10a11a12a13=4是解题的关键.
【题型】单选题
【结束】
10
【题目】若直线y=2x上存在点(x,y)满足约束条件 ,则实数m的最大值为
,则实数m的最大值为
A. -1 B. 1 C. ![]() D. 2
D. 2
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,S4=40,Sn=210,Sn-4=130,则n=( )
A.12 B.14 C.16 D.18
【答案】B
【解析】Sn-Sn-4=an+an-1+an-2+an-3=80,S4=a1+a2+a3+a4=40,所以4(a1+an)=120,a1+an=30,由Sn=![]() =210,得n=14.
=210,得n=14.
【题型】单选题
【结束】
9
【题目】等比数列{an}是递减数列,前n项的积为Tn,若T13=4T9,则a8a15=( )
A. 2 B. ±2 C. 4 D. ±4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=![]() .
.
(Ⅰ)求证:AC⊥平面BEH;
(Ⅱ)求直线PA与平面ABC所成角的正弦值.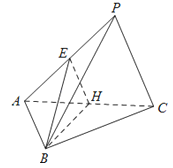
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.
(1)求抛物线准线方程;
(2)若△AOB的面积为4,求直线l的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}中,an=n2-kn(n∈N*),且{an}单调递增,则k的取值范围是( )
A. (-∞,2] B. (-∞,2) C. (-∞,3] D. (-∞,3)
【答案】D
【解析】
根据函数的单调性可得an+1﹣an>0对于n∈N*恒成立,建立关系式,解之即可求出k的取值范围.
∵数列{an}中![]() ,且{an}单调递增
,且{an}单调递增
∴an+1﹣an>0对于n∈N*恒成立即(n+1)2﹣k(n+1)﹣(n2﹣kn)=2n+1﹣k>0对于n∈N*恒成立
∴k<2n+1对于n∈N*恒成立,即k<3
故选:D.
【点睛】
本题主要考查了数列的性质,本题易错误地求导或把它当成二次函数来求解,注意n的取值是解题的关键,属于易错题.
【题型】单选题
【结束】
8
【题目】已知等差数列{an}的前n项和为Sn,S4=40,Sn=210,Sn-4=130,则n=( )
A.12 B.14 C.16 D.18
查看答案和解析>>
科目: 来源: 题型:
【题目】已知a,b,c分别是△ABC的内角A,B,C的对边,若△ABC的周长为2(![]() +1),且sin B+sin C=
+1),且sin B+sin C=![]() sin A,则a= ( )
sin A,则a= ( )
A. ![]() B. 2 C. 4 D.
B. 2 C. 4 D. ![]()
【答案】B
【解析】
根据正弦定理把![]() 转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
根据正弦定理,![]() 可化为
可化为![]()
∵△ABC的周长为![]() ,
,
∴联立方程组![]() ,
,
解得a=2.
故选:B
【点睛】
(1)在三角形中根据已知条件求未知的边或角时,要灵活选择正弦、余弦定理进行边角之间的转化,以达到求解的目的.
(2)求角的大小时,在得到角的某一个三角函数值后,还要根据角的范围才能确定角的大小,这点容易被忽视,解题时要注意.
【题型】单选题
【结束】
7
【题目】已知数列{an}中,an=n2-kn(n∈N*),且{an}单调递增,则k的取值范围是( )
A. (-∞,2] B. (-∞,2) C. (-∞,3] D. (-∞,3)
查看答案和解析>>
科目: 来源: 题型:
【题目】设二次函数f(x)=ax2+bx+c(a,b∈R)满足条件:①当x∈R时,f(x)的最大值为0,且f(x﹣1)=f(3﹣x)成立;②二次函数f(x)的图象与直线y=﹣2交于A、B两点,且|AB|=4
(Ⅰ)求f(x)的解析式;
(Ⅱ)求最小的实数n(n<﹣1),使得存在实数t,只要当x∈[n,﹣1]时,就有f(x+t)≥2x成立.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (α为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin(
(α为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin(![]() )=2
)=2![]() .
.
(Ⅰ)求曲线C和直线l在该直角坐标系下的普通方程;
(Ⅱ)动点A在曲线C上,动点B在直线l上,定点P的坐标为(﹣2,2),求|PB|+|AB|的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】关于x的不等式ax2+bx+2>0的解集为{x|-1<x<2},则关于x的不等式bx2-ax-2>0的解集为( )
A. {x|-2<x<1} B. {x|x>1或x<-2}
C. {x|x>2或x<-1} D. {x|x<-1或x>1}
【答案】B
【解析】
利用不等式的解集与方程根的关系,求出a,b的值,即可求得不等式bx2﹣ax﹣2>0的解集.
∵关于x的不等式ax2+bx+2>0的解集为(﹣1,2),
∴﹣1,2是ax2+bx+2=0(a<0)的两根
∴
∴a=﹣1,b=1
∴不等式bx2﹣ax﹣2>0为x2+x﹣2>0,
∴x<﹣2或x>1
故选:B.
【点睛】
(1)二次函数图象与x轴交点的横坐标、二次不等式解集的端点值、一元二次方程的解是同一个量的不同表现形式。
(2)二次函数、二次方程与二次不等式统称“三个二次”,它们常结合在一起,而二次函数又是“三个二次”的核心,通过二次函数的图象贯穿为一体.有关二次函数的问题,利用数形结合的方法求解,密切联系图象是探求解题思路的有效方法.
【题型】单选题
【结束】
6
【题目】已知a,b,c分别是△ABC的内角A,B,C的对边,若△ABC的周长为2(![]() +1),且sin B+sin C=
+1),且sin B+sin C=![]() sin A,则a= ( )
sin A,则a= ( )
A. ![]() B. 2 C. 4 D.
B. 2 C. 4 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com