
科目: 来源: 题型:
【题目】设f(x)=ex , f(x)=g(x)﹣h(x),且g(x)为偶函数,h(x)为奇函数,若存在实数m,当x∈[﹣1,1]时,不等式mg(x)+h(x)≥0成立,则m的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为 ![]() (a>0,β为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,直线l的极坐标方程ρcos(θ﹣
(a>0,β为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,直线l的极坐标方程ρcos(θ﹣ ![]() )=
)= ![]() .
.
(Ⅰ)若曲线C与l只有一个公共点,求a的值;
(Ⅱ)A,B为曲线C上的两点,且∠AOB= ![]() ,求△OAB的面积最大值.
,求△OAB的面积最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=mln(x+1),g(x)= ![]() (x>﹣1).
(x>﹣1).
(Ⅰ)讨论函数F(x)=f(x)﹣g(x)在(﹣1,+∞)上的单调性;
(Ⅱ)若y=f(x)与y=g(x)的图象有且仅有一条公切线,试求实数m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设M、N、T是椭圆 ![]() 上三个点,M、N在直线x=8上的摄影分别为M1、N1 .
上三个点,M、N在直线x=8上的摄影分别为M1、N1 .
(Ⅰ)若直线MN过原点O,直线MT、NT斜率分别为k1 , k2 , 求证k1k2为定值.
(Ⅱ)若M、N不是椭圆长轴的端点,点L坐标为(3,0),△M1N1L与△MNL面积之比为5,求MN中点K的轨迹方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种.若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 | A1 | A2 | A3 | A4 | A5 | A6 |
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(Ⅰ)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定a=950.记X为某同学家的一辆该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,三棱柱ABC﹣DEF中,侧面ABED是边长为2的菱形,且∠ABE= ![]() ,BC=
,BC= ![]() ,四棱锥F﹣ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM=
,四棱锥F﹣ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM= ![]() CF.
CF.
(Ⅰ)证明:直线GM∥平面DEF;
(Ⅱ)求二面角M﹣AB﹣F的余弦值.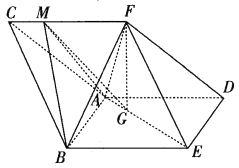
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 若Sm﹣1=﹣4,Sm=0,Sm+2=14(m≥2,且m∈N*)
(Ⅰ)求m的值;
(Ⅱ)若数列{bn}满足 ![]() =log2bn(n∈N+),求数列{(an+6)bn}的前n项和.
=log2bn(n∈N+),求数列{(an+6)bn}的前n项和.
查看答案和解析>>
科目: 来源: 题型:
【题目】非零向量 ![]() ,
, ![]() 的夹角为
的夹角为 ![]() ,且满足|
,且满足| ![]() |=λ|
|=λ| ![]() |(λ>0),向量组
|(λ>0),向量组 ![]() ,
, ![]() ,
, ![]() 由一个
由一个 ![]() 和两个
和两个 ![]() 排列而成,向量组
排列而成,向量组 ![]() ,
, ![]() ,
, ![]() 由两个
由两个 ![]() 和一个
和一个 ![]() 排列而成,若
排列而成,若 ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() 所有可能值中的最小值为4
所有可能值中的最小值为4 ![]() 2 , 则λ= .
2 , 则λ= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com