
科目: 来源: 题型:
【题目】如图1,在直角梯形ABCP中,CP∥AB,CP⊥CB,AB=BC= ![]() CP=2,D是CP的中点,将△PAD沿AD折起,使得PD⊥CD.
CP=2,D是CP的中点,将△PAD沿AD折起,使得PD⊥CD. 
(Ⅰ)若E是PC的中点,求证:AP∥平面BDE;
(Ⅱ)求证:平面PCD⊥平面ABCD;
(Ⅲ)求二面角A﹣PB﹣C的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足Sn=2an﹣2,若数列{bn}满足bn=10﹣log2an , 则使数列{bn}的前n项和取最大值时的n的值为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-5:不等式选讲
设函数f(x)=|x+2|+|x﹣1|.
(1)求f(x)的最小值及取得最小值时x的取值范围;
(2)若集合{x|f(x)+ax﹣1>0}=R,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线C1的参数方程为 ![]() (α为参数,﹣π<α<0),曲线C2的参数方程为
(α为参数,﹣π<α<0),曲线C2的参数方程为  (t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1的极坐标方程和曲线C2的普通方程;
(2)射线θ=﹣ ![]() 与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
与曲线C1的交点为P,与曲线C2的交点为Q,求线段PQ的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=(x2﹣x﹣1)ex .
(1)求函数f(x)的单调区间.
(2)若方程a( ![]() +1)+ex=ex在(0,1)内有解,求实数a的取值范围.
+1)+ex=ex在(0,1)内有解,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆E:x2+3y2=m2(m>0)的左顶点是A,左焦点为F,上顶点为B.
(1)当△AFB的面积为 ![]() 时,求m的值;
时,求m的值;
(2)若直线l交椭圆E于M,N两点(不同于A),以线段MN为直径的圆过A点,试探究直线l是否过定点,若存在定点,求出这个定点的坐标,若不存在定点,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= ![]() CD=1.
CD=1. 
(1)若M为PA中点,求证:AC∥平面MDE;
(2)若平面PAD与PBC所成的锐二面角的大小为 ![]() ,求线段PD的长度.
,求线段PD的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】持续性的雾霾天气严重威胁着人们的身体健康,汽车排放的尾气是造成雾霾天气的重要因素之一.为了贯彻落实国务院关于培育战略性新兴产业和加强节能减排工作的部署和要求,中央财政安排专项资金支持开展私人购买新能源汽车补贴试点.2017年国家又出台了调整新能源汽车推广应用财政补贴的新政策,其中新能源乘用车推广应用补贴标准如表: 某课题组从汽车市场上随机选取了20辆纯电动乘用车,根据其续驶里程R(单词充电后能行驶的最大里程,R∈[100,300])进行如下分组:第1组[100,150),第2组[150,200),第3组[200,250),第4组[250,300],制成如图所示的频率分布直方图.已知第1组与第3组的频率之比为1:4,第2组的频数为7.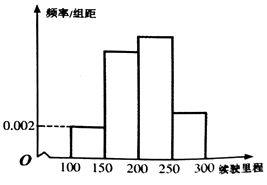
纯电动续驶里程R(公里) | 100≤R<150 | 150≤R<250 | R>250 |
补贴标准(万元/辆) | 2 | 3.6 | 44 |
(1)请根据频率分布直方图统计这20辆纯电动乘用车的平均续驶里程;
(2)若以频率作为概率,设ξ为购买一辆纯电动乘用车获得的补贴,求ξ的分布列和数学期望E(ξ).
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且b,c是关于x的一元二次方程x2+mx﹣a2+b2+c2=0的两根.
(1)求角A的大小;
(2)已知a= ![]() ,设B=θ,△ABC的面积为y,求y=f(θ)的最大值.
,设B=θ,△ABC的面积为y,求y=f(θ)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com