
科目: 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=SD=1.
(Ⅰ)证明:SD⊥平面SAB;
(Ⅱ)求AB与平面SBC所成的角的大小.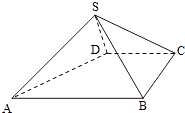
查看答案和解析>>
科目: 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 已知a1=9,a2为整数,且Sn≤S5 .
(1)求{an}的通项公式;
(2)设数列 ![]() 的前n项和为Tn , 求证:
的前n项和为Tn , 求证: ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则(写出所有正确结论编号) ①四面体ABCD每组对棱相互垂直
②四面体ABCD每个面的面积相等
③从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°而小于180°
④连接四面体ABCD每组对棱中点的线段互垂直平分
⑤从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在锐角三角形ABC 中,角 A,B,C 的对边分别为 a,b,c.若a=2bsinC,则tanA+tanB+tanC的最小值是( )
A.4
B.![]()
C.8
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知双曲线 ![]() 的两条渐近线分别为l1 , l2 , 经过右焦点F垂直于l1的直线分别交l1 , l2 于 A,B 两点.若|
的两条渐近线分别为l1 , l2 , 经过右焦点F垂直于l1的直线分别交l1 , l2 于 A,B 两点.若| ![]() |,|
|,| ![]() |,|
|,| ![]() |成等差数列,且
|成等差数列,且 ![]() 与
与 ![]() 反向,则该双曲线的离心率为( )
反向,则该双曲线的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=|x|+|x+1|.
(1)若x∈R,恒有f(x)≥λ成立,求实数λ的取值范围;
(2)若m∈R,使得m2+2m+f(t)=0成立,试求实数t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xoy中,直线的参数方程为 ![]() (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程,并指出其表示何种曲线;
(2)设直线l与曲线C交于A,B两点,若点P的直角坐标为(1,0),试求当 ![]() 时,|PA|+|PB|的值.
时,|PA|+|PB|的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数g(x)= ![]() +g(x).
+g(x).
(1)试判断g(x)的单调性;
(2)若f(x)在区间(0,1)上有极值,求实数a的取值范围;
(3)当a>0时,若f(x)有唯一的零点x0 , 试求[x0]的值.(注:[x]为取整函数,表示不超过x的最大整数,如[0.3]=0,[2.6]=2,[﹣1.4]=﹣2;以下数据供参考:ln2=0.6931,ln3=1.099,ln5=1.609,ln7=1.946)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C: ![]() 的一个焦点为F(3,0),其左顶点A在圆O:x2+y2=12上.
的一个焦点为F(3,0),其左顶点A在圆O:x2+y2=12上.
(1)求椭圆C的方程;
(2)直线l:x=my+3(m≠0)交椭圆C于M,N两点,设点N关于x轴的对称点为N1(点N1与点M不重合),且直线N1M与x轴的交于点P,试问△PMN的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD= ![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°. 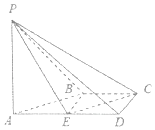
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P﹣CD﹣A的大小为45°,求二面角P﹣CE﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com