
科目: 来源: 题型:
【题目】设椭圆 ![]() =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为 ![]() ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为 ![]() .
.
(1)求椭圆的方程;
(2)设A,B分别为椭圆的左,右顶点,过点F且斜率为k的直线与椭圆交于C,D两点.若 ![]() =8,求k的值.
=8,求k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点. 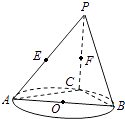
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足 ![]() .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=x3+ax2+bx+c.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)设a=b=4,若函数f(x)有三个不同零点,求c的取值范围;
(3)求证:a2﹣3b>0是f(x)有三个不同零点的必要而不充分条件.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人组成“星队”参加猜成语活动,每轮活动由甲、乙各猜一个成语,在一轮活动中,如果两人都猜对,则“星队”得3分;如果只有一个人猜对,则“星队”得1分;如果两人都没猜对,则“星队”得0分.已知甲每轮猜对的概率是 ![]() ,乙每轮猜对的概率是
,乙每轮猜对的概率是 ![]() ;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
;每轮活动中甲、乙猜对与否互不影响.各轮结果亦互不影响.假设“星队”参加两轮活动,求:
(1)“星队”至少猜对3个成语的概率;
(2)“星队”两轮得分之和为X的分布列和数学期望EX.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) 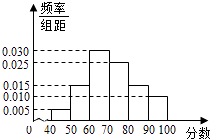
A.588
B.480
C.450
D.120
查看答案和解析>>
科目: 来源: 题型:
【题目】若将函数y=2sin 2x的图像向左平移 ![]() 个单位长度,则评议后图象的对称轴为( )
个单位长度,则评议后图象的对称轴为( )
A.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目: 来源: 题型:
【题目】(2015·湖南)某工作的三视图如图3所示,现将该工作通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工作的一个面内,则原工件材料的利用率为(材料利用率=新工件的体积/原工件的体积)
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C1:x2=4y 的焦点F也是椭圆c2:![]() 的一个焦点, C1和C2的公共弦长为
的一个焦点, C1和C2的公共弦长为![]()
(1)求 C2的方程;
(2)过点F 的直线 l与 C1相交于A与B两点, 与C2相交于C , D两点,且![]() 与
与![]() 同向
同向
(ⅰ)若 ![]() 求直线l的斜率;
求直线l的斜率;
(ⅱ)设 C1在点 A处的切线与 x轴的交点为M ,证明:直线l 绕点 F旋转时, ![]() MFD总是钝角三角形。
MFD总是钝角三角形。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知四棱台![]() 上、下底面分别是边长为3和6的正方形,
上、下底面分别是边长为3和6的正方形,![]() ,且
,且![]() 底面
底面![]() ,点
,点![]() ,
,![]() 分别在棱
分别在棱![]() ,
,![]() 上.
上.
(1)若是![]() 是
是![]() 的中点,证明:
的中点,证明:![]() ;
;
(2若![]() //平面
//平面![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() ,求四面体
,求四面体![]() 的体积
的体积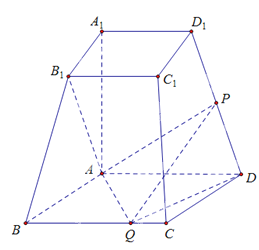
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com