
科目: 来源: 题型:
【题目】如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2. 
(1)求证:平面ABF⊥平面PQFE;
(2)若PQ与平面ABF所成的角为 ![]() ,求三棱锥P﹣QDE的体积.
,求三棱锥P﹣QDE的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】城市发展面临生活垃圾产生量逐年剧增的困扰,为了建设宜居城市,2017年1月,某市制定《生活垃圾分类和减量工作方案》,到2020年,生活垃圾无害化处理率达到100%.如图是该市2011~2016年生活垃圾年产生量(单位:万吨)的柱状图;如表是2016年年初与年末对该市四个社区各随机抽取1000人调查参与垃圾分类人数的统计表: 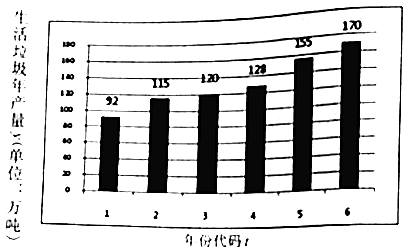
2016年初 | 2016年末 | |
社区A | 539 | 568 |
社区B | 543 | 585 |
社区C | 568 | 600 |
社区D | 496 | 513 |
注1:年份代码1~6分别对应年份2011~2016
注2:参与度= ![]() ×100%
×100%
参与度的年增加值=年末参与度﹣年初参与度
(1)由图可看出,该市年垃圾生产量y与年份代码t之间具有较强的线性相关关系,运用最小二乘法可得回归直线方程为 ![]() =14.8t+
=14.8t+ ![]() ,预测2020年该年生活垃圾的产生量;
,预测2020年该年生活垃圾的产生量;
(2)已知2016年该市生活在垃圾无害化化年处理量为120万吨,且全市参与度每提高一个百分点,都可使该市的生活垃圾无害化处理量增加6万吨,用样本估计总体的思想解决以下问题: ①由表的数据估计2016年该市参与度的年增加值,假设2017年该市参与度的年增加值与2016年大致相同,预测2017年全市生活垃圾无害化处理量;
②在2017年的基础上,若2018年至2020年的参与度逐年增加5个百分点,则到2020年该市能否实现生活垃圾无害化处理率达到100%的目标?
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别为a,b,c,满足(2a﹣c)cosB=bcosC. 
(1)求B的大小;
(2)如图,AB=AC,在直线AC的右侧取点D,使得AD=2CD=4.当角D为何值时,四边形ABCD面积最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=(x﹣a)(x﹣b)(x﹣c)(其中a>1,b>1),x=0是f(x)的一个零点,曲线y=f(x)在点(1,f(1))处的切线平行于x轴,则a+b的最小值为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知随圆E: ![]() +
+ ![]() =1(a>b>0)与过原点的直线交于A、B两点,右焦点为F,∠AFB=120°,若△AFB的面积为4
=1(a>b>0)与过原点的直线交于A、B两点,右焦点为F,∠AFB=120°,若△AFB的面积为4 ![]() ,则椭圆E的焦距的取值范围是( )
,则椭圆E的焦距的取值范围是( )
A.[2,+∞)
B.[4,+∞)
C.[2 ![]() ,+∞)
,+∞)
D.[4 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知双曲线的中心在原点O,左焦点为F1 , 圆O过点F1 , 且与双曲线的一个交点为P,若直线PF1的斜率为 ![]() ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.y=±x
B.y=± ![]() x
x
C.y=± ![]() x
x
D.y=± ![]() x
x
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,已知点P(2,0),曲线C的参数方程为 ![]() (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线C的普通方程和极坐标方程;
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线C的普通方程和极坐标方程;
(Ⅱ)过点P且倾斜角为 ![]() 的直线l交曲线C于A,B两点,求|AB|.
的直线l交曲线C于A,B两点,求|AB|.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=(x﹣3)ex+ax,a∈R. (Ⅰ)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;
(Ⅱ)当a∈[0,e)时,设函数f(x)在(1,+∞)上的最小值为g(a),求函数g(a)的值域.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,短轴长为2. (Ⅰ)求椭圆C的标准方程;
,短轴长为2. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)若圆O:x2+y2=1的切线l与曲线E相交于A、B两点,线段AB的中点为M,求|OM|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com