【题目】函数f（x）=x|x|．若存在x∈[1，+∞），使得f（x﹣2k）﹣k＜0，则k的取值范围是（ ）
A.（2，+∞）
B.（1，+∞）
C.（ ，+∞）
D.（ ，+∞）

【题目】已知椭圆C： =1（a＞b＞0）的离心率是 ，且过点 ．直线y= x+m与椭圆C相交于A，B两点． （Ⅰ）求椭圆C的方程；
（Ⅱ）求△PAB的面积的最大值；
（Ⅲ）设直线PA，PB分别与y轴交于点M，N．判断|PM|，|PN|的大小关系，并加以证明．

【题目】已知函数 ，其中a∈R． （Ⅰ）给出a的一个取值，使得曲线y=f（x）存在斜率为0的切线，并说明理由；
（Ⅱ）若f（x）存在极小值和极大值，证明：f（x）的极小值大于极大值．

【题目】如图，在几何体ABCDEF中，底面ABCD为矩形，EF∥CD，CD⊥EA，CD=2EF=2，ED= ．M为棱FC上一点，平面ADM与棱FB交于点N．
（Ⅰ）求证：ED⊥CD；
（Ⅱ）求证：AD∥MN；
（Ⅲ）若AD⊥ED，试问平面BCF是否可能与平面ADMN垂直？若能，求出 的值；若不能，说明理由．

【题目】设{an}是首项为1，公差为2的等差数列，{bn}是首项为1，公比为q的等比数列．记cn=an+bn ， n=1，2，3，…．
（1）若{cn}是等差数列，求q的值；
（2）求数列{cn}的前n项和Sn ．

（Ⅰ）在抽样的100人中，求对A餐厅评分低于30的人数；
（Ⅱ）从对B餐厅评分在[0，20）范围内的人中随机选出2人，求2人中恰有1人评分在[0，10）范围内的概率；
（Ⅲ）如果从A，B两家餐厅中选择一家用餐，你会选择哪一家？说明理由．

【题目】已知函数 ． （Ⅰ）求f（x）的定义域；
（Ⅱ）设β是锐角，且 ，求β的值．

【题目】函数f（x）=x|x|．若存在x∈[1，+∞），使得f（x﹣2k）﹣k＜0，则k的取值范围是（ ）
A.（2，+∞）
B.（1，+∞）
C.（ ，+∞）
D.（ ，+∞）

【题目】如图1所示，在等腰梯形ABCD中， ．把△ABE沿BE折起，使得 ，得到四棱锥A﹣BCDE．如图2所示．
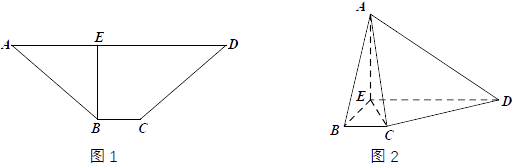
（1）求证：面ACE⊥面ABD；
（2）求平面ABE与平面ACD所成锐二面角的余弦值．