
科目: 来源: 题型:
【题目】若函数f(x)= ![]() . (a>0且a≠1),函数g(x)=f(x)﹣k.
. (a>0且a≠1),函数g(x)=f(x)﹣k.
①若a= ![]() ,函数g(x)无零点,则实数k的取值范围为;
,函数g(x)无零点,则实数k的取值范围为;
②若f(x)有最小值,则实数a的取值范围是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】在空间直角坐标系O﹣xyz中,已知A(2,0,0),B(0,2,0),C(0,0,0),P(0,1, ![]() ),则三棱锥P﹣ABC在坐标平面xOz上的正投影图形的面积为;该三棱锥的最长棱的棱长为 .
),则三棱锥P﹣ABC在坐标平面xOz上的正投影图形的面积为;该三棱锥的最长棱的棱长为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】四支足球队进行单循环比赛(每两队比赛一场),每场比赛胜者得3分,负者得0分,平局双方各得1分.比赛结束后发现没有足球队全胜,且四队得分各不相同,则所有比赛中最多可能出现的平局场数是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目: 来源: 题型:
【题目】第五届北京农业嘉年华于2017年3月11日至5月7日在昌平区兴寿镇草莓博览园中举办,设置“三馆两园一带一谷一线”八大功能板块.现安排六名志愿者去其中的“三馆两园”参加志愿者服务工作,若每个“馆”与“园”都至少安排一人,则不同的安排方法种数为( )
A.C ![]() A
A ![]()
B.5C ![]() A
A ![]()
C.5A ![]()
D.C ![]() A
A ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】命题p:数列{an}的前n项和Sn=an2+bn+c(a≠0);命题q:数列{an}是等差数列.则p是q的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目: 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为 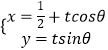 ,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A,B两点,当θ变化时,求|AB|的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=(x﹣2)ex﹣ ![]() x2 , 其中a∈R,e为自然对数的底数
x2 , 其中a∈R,e为自然对数的底数
(Ⅰ)函数f(x)的图象能否与x轴相切?若能与x轴相切,求实数a的值;否则,请说明理由;
(Ⅱ)若函数y=f(x)+2x在R上单调递增,求实数a能取到的最大整数值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆C1:x2+y2=r2(r>0)与直线l0:y= ![]() 相切,点A为圆C1上一动点,AN⊥x轴于点N,且动点M满足
相切,点A为圆C1上一动点,AN⊥x轴于点N,且动点M满足 ![]() ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C.
(1)求动点M的轨迹曲线C的方程;
(2)若直线l与曲线C相交于不同的两点P、Q且满足以PQ为直径的圆过坐标原点O,求线段PQ长度的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD, ![]() ,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.
,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.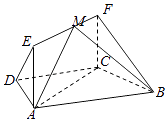
(1)求证:EF⊥平面BCF;
(2)点M在线段EF(含端点)上运动,当点M在什么位置时,平面MAB与平面FCB所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com