
科目: 来源: 题型:
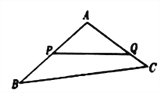
【题目】如图,某生态园将一块三角形地![]() 的一角
的一角![]() 开辟为水果园,已知角
开辟为水果园,已知角![]() 为
为![]() ,
, ![]() 的长度均大于200米,现在边界
的长度均大于200米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
(1)若围墙![]() 、
、![]() 总长度为200米,如何可使得三角形地块
总长度为200米,如何可使得三角形地块![]() 面积最大?
面积最大?
(2)已知竹篱笆长为![]() 米,
米, ![]() 段围墙高1米,
段围墙高1米, ![]() 段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
查看答案和解析>>
科目: 来源: 题型:
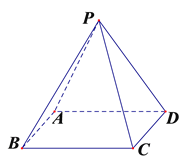
【题目】如图在四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD![]() 底面ABCD,
底面ABCD, ![]() ;
;
(1)求证:平面PAB![]() 平面PCD;
平面PCD;
(2)若过点B的直线![]() 垂直平面PCD,求证:
垂直平面PCD,求证: ![]() //平面PAD.
//平面PAD.
查看答案和解析>>
科目: 来源: 题型:
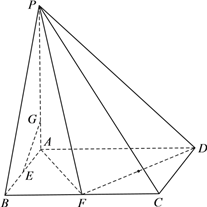
【题目】如图,四棱锥P-ABCD中,底面ABCD是矩形,PA![]() 面ABCD,且AB=2,AD=4,
面ABCD,且AB=2,AD=4,
AP=4,F是线段BC的中点.
⑴ 求证:面PAF![]() 面PDF;
面PDF;
⑵ 若E是线段AB的中点,在线段AP上是否存在一点G,使得EG![]() 面PDF?若存在,求出线段AG的长度;若不存在,说明理由.
面PDF?若存在,求出线段AG的长度;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某公司生产某产品的年固定成本为100万元,每生产1千件需另投入27万元,设该公司一年内生产该产品![]() 千件
千件![]() 并全部销售完,每千件的销售收入为
并全部销售完,每千件的销售收入为![]() 万元,且
万元,且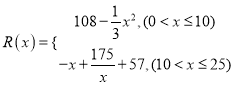 .
.
⑴ 写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
⑵ 当年产量为多少千件时,该公司在这一产品的生产中所获年利润最大?(注:年利润=年销售收入![]() 年总成本).
年总成本).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() ,抛物线
,抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上, ![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上各取两个点,其坐标分别是
,从每条曲线上各取两个点,其坐标分别是![]() ,
, ![]() ,
, ![]() ,
, 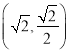 .
.
(1)求![]() ,
, ![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交于不同的两点
交于不同的两点![]() 且满足
且满足![]() ?若存在,求出直线方程;若不存在,请说明理由.
?若存在,求出直线方程;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
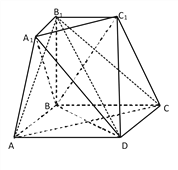
【题目】如图所示的几何体是由棱台![]() 和棱锥
和棱锥![]() 拼接而成的组合体,其底面四边形
拼接而成的组合体,其底面四边形![]() 是边长为
是边长为![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求证:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校举办“中国诗词大赛”活动,某班派出甲乙两名选手同时参加比赛. 大赛设有15个诗词填空题,其中“唐诗”、“宋词”和“毛泽东诗词”各5个.每位选手从三类诗词中各任选1个进行作答,3个全答对选手得3分,答对2个选手得2分,答对1个选手得1分,一个都没答对选手得0分. 已知“唐诗”、“宋词”和“毛泽东诗词”中甲能答对的题目个数依次为5,4,3,乙能答对的题目个数依此为4,5,4,假设每人各题答对与否互不影响,甲乙两人答对与否也互不影响.
求:(1)甲乙两人同时得到3分的概率;
(2)甲乙两人得分之和![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市根据地理位置划分成了南北两区,为调查该市的一种经济作物![]() (下简称
(下简称![]() 作物)的生长状况,用简单随机抽样方法从该市调查了 500 处
作物)的生长状况,用简单随机抽样方法从该市调查了 500 处 ![]() 作物种植点,其生长状况如表:
作物种植点,其生长状况如表:

其中生长指数的含义是:2 代表“生长良好”,1 代表“生长基本良好”,0 代表“不良好,但仍有收成”,﹣1代表“不良好,绝收”.
(1)估计该市空气质量差的![]() 作物种植点中,不绝收的种植点所占的比例;
作物种植点中,不绝收的种植点所占的比例;
(2)能否有 99%的把握认为“该市![]() 作物的种植点是否绝收与所在地域有关”?
作物的种植点是否绝收与所在地域有关”?
(3)根据(2)的结论,能否提供更好的调查方法来估计该市![]() 作物的种植点中,绝收种植点的比例?请说明理由.
作物的种植点中,绝收种植点的比例?请说明理由.


查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求![]() 的方程;
的方程;
(2)若动点![]() 在直线
在直线![]() 上,过
上,过![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() 两点,使得
两点,使得![]() ,再过
,再过![]() 作直线
作直线![]() ,证明:直线
,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com