
科目: 来源: 题型:
【题目】在一个不透明的箱子里装有5个完全相同的小球,球上分别标有数字1、2、3、4、5.甲先从箱子中摸出一个小球,记下球上所标数字后,将该小球放回箱子中摇匀后,乙再从该箱子中摸出一个小球.
(1)若甲、乙两人谁摸出的球上标的数字大谁就获胜(数字相同为平局),求甲获胜的概率;
(2)规定:两人摸到的球上所标数字之和小于6,则甲获胜,否则乙获胜,这样规定公平吗?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校夏令营有3名男同学A、B、C和3名女同学X,Y,Z,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
(1)用表中字母列举出所有可能的结果;
(2)设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M发生的概率.
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中;5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数,据此估计,该运动员三次投篮恰有两次命中的概率为( )
137 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
A.0.40 B.0.30 C.0.35 D.0.25
查看答案和解析>>
科目: 来源: 题型:
【题目】“抛阶砖”是国外游乐场的典型游戏之一.参与者只需将手上的“金币”(设“金币”的半径为1)抛向离身边若干距离的阶砖平面上,抛出的“金币”若恰好落在任何一个阶砖(边长为2.1的正方形)的范围内(不与阶砖相连的线重叠),便可获大奖.不少人被高额奖金所吸引,纷纷参与此游戏,但很少有人得到奖品,请用所学的概率知识解释这是为什么.
查看答案和解析>>
科目: 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤.
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
查看答案和解析>>
科目: 来源: 题型:
【题目】一台机器由于使用时间较长,生产的零件有一些缺损,按不同转速生产出来的零件有缺损的统计数据如下表所示.
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围内?
转速x(转/秒) | 16 | 14 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目: 来源: 题型:
【题目】要分析学生初中升学考试的数学成绩对高一年级数学学习有什么影响,在高一年级学生中随机抽取10名学生,分析他们入学的数学成绩(x)和高一年级期末数学考试成绩(y)(如下表):
(1)画出散点图;
(2)判断入学成绩(x)与高一期末考试成绩(y)是否有线性相关关系;
(3)如果x与y具有线性相关关系,求出回归直线方程;
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
x | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
y | 65 | 78 | 52 | 85 | 92 | 89 | 73 | 98 | 56 | 75 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆锥曲线![]() :
: 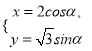 (
(![]() 为参数)和定点
为参数)和定点![]() ,
, ![]() ,
, ![]() 是此圆锥曲线
是此圆锥曲线![]() 的左、右焦点.
的左、右焦点.
(1)以原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,求直线
轴的正半轴为极轴建立极坐标系,求直线![]() 的极坐标方程;
的极坐标方程;
(2)经过![]() 且与直线
且与直线![]() 垂直的直线交此圆锥曲线
垂直的直线交此圆锥曲线![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的极小值;
的极小值;
(Ⅱ)在(Ⅰ)的条件下,是否存在实常数![]() 和
和![]() ,使得
,使得![]() 和
和![]() ?若存在,求出
?若存在,求出![]() 和
和![]() 的值.若不存在,说明理由;
的值.若不存在,说明理由;
(Ⅲ)设![]() 有两个零点
有两个零点![]() ,且
,且![]() 成等差数列,试探究
成等差数列,试探究![]() 值的符号.
值的符号.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com