练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一台机器由于使用时间较长，生产的零件有一些缺损，按不同转速生产出来的零件有缺损的统计数据如下表所示.

    (1)作出散点图；

    (2)如果y与x线性相关，求出回归直线方程；

    (3)若实际生产中，允许每小时的产品中有缺损的零件最多为10个，那么机器的运转速度应控制在什么范围内？

    转速x(转/秒)

    16

    14

    12

    8

    每小时生产有缺损零件数y(个)

    11

    9

    8

    5

    【答案】（1）见解析 （2）＝0.73x－0.875 （3）15转/秒

    【解析】 (1)作散点图如图所示．

    (2)由散点图可知y与x线性相关，故可设回归直线方程为＝bx＋a.

    可算得，＝12.5，＝8.25，，，

    ∴，a＝－b≈8.25－0.73×12.5＝－0.875.

    ∴所求回归直线方程为＝0.73x－0.875.

    (3)令＝10，得0.73x－0.875＝10，解得x≈15.

    即机器的运转速度应控制在15转/秒内．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数， .

    (1)求函数的最小正周期；

    (2)求函数在区间上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设△ABC的内角A，B，C所对的边分别为a，b，c，满足．

    (1)求角C的大小；

    (2)设函数f(x)＝cos(2x＋C)，将f(x)的图象向右平移个单位长度后得到函数g(x)的图象，求函数g(x)在区间上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列的前项和为， ， 为整数，且对任意都有．

    （1）求的通项公式；

    （2）设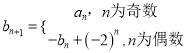， 求的前项和；

    （3）在（2）的条件下，若数列满足．是否存在实数，使得数列是单调递增数列．若存在，求出的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列为递增的等比数列, ，

    数列满足．

    （Ⅰ）求数列的通项公式；（Ⅱ）求证： 是等差数列；

    （Ⅲ）设数列满足，且数列的前项和，并求使得对任意都成立的正整数的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一个不透明的箱子里装有5个完全相同的小球，球上分别标有数字1、2、3、4、5．甲先从箱子中摸出一个小球，记下球上所标数字后，将该小球放回箱子中摇匀后，乙再从该箱子中摸出一个小球．

    （1）若甲、乙两人谁摸出的球上标的数字大谁就获胜（数字相同为平局），求甲获胜的概率；

    （2）规定：两人摸到的球上所标数字之和小于6，则甲获胜，否则乙获胜，这样规定公平吗？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个地区共有5个乡镇，共30万人，其人口比例为3∶2∶5∶2∶3，从这30万人中抽取一个300人的样本，分析某种疾病的发病率.已知这种疾病与不同的地理位置及水土有关，则应采取什么样的抽样方法?并写出具体过程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆过点，且离心率．

    （Ⅰ）求椭圆的方程．

    （Ⅱ）若椭圆上存在点、关于直线对称，求的所有取值构成的集合，并证明对于， 的中点恒在一条定直线上．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中，底面是等腰直角三角形， ，侧棱，点分别为棱的中点， 的重心为，直线垂直于平面.

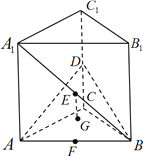
    （1）求证：直线平面；

    （2）求二面角的余弦.

    查看答案和解析>>

    同步练习册答案