
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() 为整数,且对任意
为整数,且对任意![]() 都有
都有![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,
, 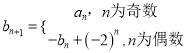 求
求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,若数列![]() 满足
满足![]() .是否存在实数
.是否存在实数![]() ,使得数列
,使得数列![]() 是单调递增数列.若存在,求出
是单调递增数列.若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在 ![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点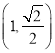 ,离心率为
,离心率为![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 的长轴的两个端点(
的长轴的两个端点(![]() 位于
位于![]() 右侧),
右侧),![]() 是椭圆在
是椭圆在![]() 轴正半轴上的顶点.
轴正半轴上的顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 和
和![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出直线方程;如果不存在,请说明理由.
共线?如果存在,求出直线方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩阵![]() 将直线l:x+y-1=0变换成直线l′.
将直线l:x+y-1=0变换成直线l′.
(1)求直线l′的方程;
(2)判断矩阵A是否可逆?若可逆,求出矩阵A的逆矩阵A-1;若不可逆,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着高等级公路的迅速发展,公路绿化受到高度重视,需要大量各种苗木.某苗圃培植场对100棵“天竺桂”的移栽成活量![]() (单位:棵)与在前三个月内浇水次数
(单位:棵)与在前三个月内浇水次数![]() 间的关系进行研究,根据以往的记录,整理相关的数据信息如图所示:
间的关系进行研究,根据以往的记录,整理相关的数据信息如图所示:

(1)结合图中前4个矩形提供的数据,利用最小二乘法求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)用![]() 表示(1)中所求的回归直线方程得到的100棵“天竺桂”的移栽成活量的估计值,当图中余下的矩形对应的数据组
表示(1)中所求的回归直线方程得到的100棵“天竺桂”的移栽成活量的估计值,当图中余下的矩形对应的数据组![]() 的残差的绝对值
的残差的绝对值![]() ,则回归直线方程有参考价值,试问:(1)中所得到的回归直线方程有参考价值吗?
,则回归直线方程有参考价值,试问:(1)中所得到的回归直线方程有参考价值吗?
(3)预测100棵“天竺桂”移栽后全部成活时,在前三个月内浇水的最佳次数.
附:回归直线方程为![]() ,其中
,其中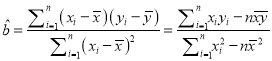 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线![]() :
:  (
(![]() 为参数)和定点
为参数)和定点![]() ,
, ![]() ,
, ![]() 是此圆锥曲线
是此圆锥曲线![]() 的左、右焦点.
的左、右焦点.
(1)以原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,求直线
轴的正半轴为极轴建立极坐标系,求直线![]() 的极坐标方程;
的极坐标方程;
(2)经过![]() 且与直线
且与直线![]() 垂直的直线交此圆锥曲线
垂直的直线交此圆锥曲线![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器由于使用时间较长,生产的零件有一些缺损,按不同转速生产出来的零件有缺损的统计数据如下表所示.
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么机器的运转速度应控制在什么范围内?
转速x(转/秒) | 16 | 14 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,点
,点![]() 分别为棱
分别为棱![]() 的中点,
的中点, ![]() 的重心为
的重心为![]() ,直线
,直线![]() 垂直于平面
垂直于平面![]() .
.
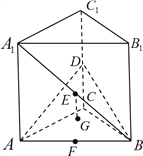
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦.
的余弦.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数![]() 在区间
在区间![]() 上的图象,为了得到这个函数的图象,只需将y=sinx的图象
上的图象,为了得到这个函数的图象,只需将y=sinx的图象

A. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
B. 向左平移至![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
C. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
D. 向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com