
【题目】已知曲线![]() .
.
(1)若曲线C在点![]() 处的切线为
处的切线为![]() ,求实数
,求实数![]() 和
和![]() 的值;
的值;
(2)对任意实数![]() ,曲线
,曲线![]() 总在直线
总在直线![]() :
:![]() 的上方,求实数
的上方,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ,(2)
,(2)![]() .
.
【解析】
试题分析:(1)根据导数几何意义,所以![]() .因为
.因为![]() ,所以
,所以![]() .因为
.因为![]() 过点
过点![]() ,所以
,所以![]() ,(2)由题意得:不等式
,(2)由题意得:不等式![]() 恒成立,恒成立问题一般转化为最值问题.一是分类讨论求函数
恒成立,恒成立问题一般转化为最值问题.一是分类讨论求函数![]() 最小值,二是变量分离为
最小值,二是变量分离为![]() 恒成立,求函数
恒成立,求函数![]() 最小值.两种方法都是
最小值.两种方法都是![]() ,然后对实数a进行讨论,当
,然后对实数a进行讨论,当![]() 时,
时,![]() ,所以
,所以![]() .当
.当![]() 时,由
时,由![]() 得
得![]() ,不论
,不论![]() 还是
还是![]() ,
,![]() 都是先减后增,即
都是先减后增,即![]() 的最小值为
的最小值为![]() ,所以
,所以![]() .
.
试题解析:解
(1)![]() , 2分
, 2分
因为曲线C在点(0,1)处的切线为L:![]() ,
,
所以![]() 且
且![]() . 4分
. 4分
解得![]() ,
,![]() -5分
-5分
(2)法1:
对于任意实数a,曲线C总在直线的![]() 的上方,等价于
的上方,等价于
x,![]() ,都有
,都有![]() ,
,
即x,![]() R,
R,![]() 恒成立, 6分
恒成立, 6分
令![]() , 7分
, 7分
①若a=0,则![]() ,
,
所以实数b的取值范围是![]() ; 8分
; 8分
②若![]() ,
,![]() ,
,
由![]() 得
得![]() , 9分
, 9分
![]() 的情况如下:
的情况如下:
|
| 0 |
|
|
| 0 | + |
|
| 极小值 |
|
11分
所以![]() 的最小值为
的最小值为![]() , 12分
, 12分
所以实数b的取值范围是![]() ;
;
综上,实数b的取值范围是![]() . 13分
. 13分
法2:对于任意实数a,曲线C总在直线的![]() 的上方,等价于
的上方,等价于
x,![]() ,都有
,都有![]() ,即
,即
x,![]() R,
R,![]() 恒成立, 6分
恒成立, 6分
令![]() ,则等价于
,则等价于![]() ,
,![]() 恒成立,
恒成立,
令![]() ,则
,则![]() , 7分
, 7分
由![]() 得
得![]() , 9分
, 9分
![]() 的情况如下:
的情况如下:
|
| 0 |
|
|
| 0 | + |
|
| 极小值 |
|
-11分
所以![]() 的最小值为
的最小值为![]() , 12分
, 12分
实数b的取值范围是![]() . 13分
. 13分


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】某市根据地理位置划分成了南北两区,为调查该市的一种经济作物![]() (下简称
(下简称![]() 作物)的生长状况,用简单随机抽样方法从该市调查了 500 处
作物)的生长状况,用简单随机抽样方法从该市调查了 500 处 ![]() 作物种植点,其生长状况如表:
作物种植点,其生长状况如表:

其中生长指数的含义是:2 代表“生长良好”,1 代表“生长基本良好”,0 代表“不良好,但仍有收成”,﹣1代表“不良好,绝收”.
(1)估计该市空气质量差的![]() 作物种植点中,不绝收的种植点所占的比例;
作物种植点中,不绝收的种植点所占的比例;
(2)能否有 99%的把握认为“该市![]() 作物的种植点是否绝收与所在地域有关”?
作物的种植点是否绝收与所在地域有关”?
(3)根据(2)的结论,能否提供更好的调查方法来估计该市![]() 作物的种植点中,绝收种植点的比例?请说明理由.
作物的种植点中,绝收种植点的比例?请说明理由.


查看答案和解析>>
科目:高中数学 来源: 题型:
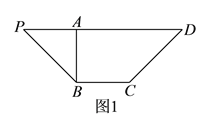
【题目】如图![]() ,等腰梯形
,等腰梯形![]() 中,
中, ![]() ,
, ![]() 于点
于点![]() ,
, ![]() ,且
,且![]() .沿
.沿![]() 把
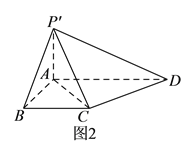
把![]() 折起到
折起到![]() 的位置(如图
的位置(如图![]() ),使
),使![]() .
.
(I)求证: ![]() 平面
平面![]() .
.
(II)求三棱锥![]() 的体积.
的体积.
(III)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,指出点
,若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的标准方程为
的标准方程为![]() ,离心率
,离心率![]() ,且椭圆经过点
,且椭圆经过点![]() .过右焦点
.过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,求直线
,求直线![]() 的方程.
的方程.
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() ,
, ![]() 为邻边的四边形
为邻边的四边形![]() 是菱形,且点
是菱形,且点![]() 在椭圆上.若存在,求出
在椭圆上.若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() 为整数,且对任意
为整数,且对任意![]() 都有
都有![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,
, 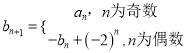 求
求![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,若数列![]() 满足
满足![]() .是否存在实数
.是否存在实数![]() ,使得数列
,使得数列![]() 是单调递增数列.若存在,求出
是单调递增数列.若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com