
【题目】如图![]() ,等腰梯形
,等腰梯形![]() 中,
中, ![]() ,
, ![]() 于点
于点![]() ,
, ![]() ,且
,且![]() .沿
.沿![]() 把
把![]() 折起到
折起到![]() 的位置(如图
的位置(如图![]() ),使
),使![]() .
.
(I)求证: ![]() 平面
平面![]() .
.
(II)求三棱锥![]() 的体积.
的体积.
(III)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,指出点
,若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
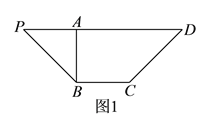
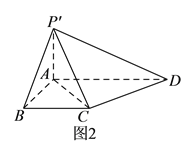
【答案】(I)见解析;(II)![]() ;(III)存在
;(III)存在![]() ,
, ![]() 为
为![]() 中点.
中点.
【解析】试题分析:(Ⅰ)推导出![]() ⊥AD,AB⊥
⊥AD,AB⊥![]() .从而
.从而![]() ⊥面ABCD.进而
⊥面ABCD.进而![]() ⊥CD,再求出AC⊥CD.由此能证明CD⊥平面
⊥CD,再求出AC⊥CD.由此能证明CD⊥平面![]() .
.
(Ⅱ)由VA-P'BC=VP'-ABC,能求出三棱锥A-P'BC的体积.
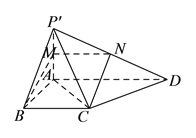
(Ⅲ)取P'A中点M,P'D中点N,连结BM,MN,NC,推导出四边形BCNM为平行四边形,由此能求出存在一点M,M为![]() 的中点,使得BM∥面
的中点,使得BM∥面![]() CD.
CD.
试题解析:(I)∵![]() ,故
,故![]() ,
,
∵在等腰梯形中, ![]() ,
,
∴在四棱锥中, ![]() ,
,
又∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵等腰梯形![]() 中,
中,
![]() ,
, ![]() ,
,
且![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() .
.
(II)![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
![]() .
.
(III)存在点![]() ,
, ![]() 为
为![]() 中点,使得
中点,使得![]() 平面
平面![]() ,
,
证明:取![]() ,
, ![]() 中点为
中点为![]() ,
, ![]() ,
,
连接![]() ,
, ![]() ,
, ![]() ,
,
∵![]() ,
, ![]() 是
是![]() ,
, ![]() 中点,
中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() 面
面![]() ,
,
![]() 面
面![]() ,
,
∴![]() 平面
平面![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,经过椭圆
中,经过椭圆![]() :
: ![]() 的一个焦点的直线
的一个焦点的直线![]() 与
与![]() 相交于
相交于![]() 两点,
两点, ![]() 为
为![]() 的中点,且
的中点,且![]() 斜率是
斜率是![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)直线![]() 分别与椭圆
分别与椭圆![]() 和圆
和圆![]() :
: ![]() 相切于点
相切于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,短轴长为
轴上,短轴长为![]() ,且两个焦点和短轴的两个端点恰为一个正方形的顶点,过右焦点
,且两个焦点和短轴的两个端点恰为一个正方形的顶点,过右焦点![]() 与
与![]() 轴不垂直的直线交椭圆于
轴不垂直的直线交椭圆于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的方程.
(Ⅱ)当直线![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 的面积.
的面积.
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得经
,使得经![]() ,
, ![]() 为领边的平行四边形是菱形?若存在,求出
为领边的平行四边形是菱形?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为
的方程为![]() (
(![]() ,
, ![]() 为常数).
为常数).
(1)判断曲线![]() 的形状;
的形状;
(2)设曲线![]() 分别与
分别与![]() 轴,
轴, ![]() 轴交于点
轴交于点![]() ,
, ![]() (
(![]() ,
, ![]() 不同于原点
不同于原点![]() ),试判断
),试判断![]() 的面积
的面积![]() 是否为定值?并证明你的判断;
是否为定值?并证明你的判断;
(3)设直线![]() :
: ![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线l过点P(-3,2),倾斜角为![]() ,且
,且![]() .曲线C的参数方程为
.曲线C的参数方程为![]() (
(![]() 为参数).直线l与曲线C交于A、B两点,线段AB的中点为M.
为参数).直线l与曲线C交于A、B两点,线段AB的中点为M.
(Ⅰ)求直线l的参数方程和曲线C的普通方程;
(Ⅱ)求线段PM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的身体状况,某校随机抽取了一批学生测量体重,经统计,这批学生的体重数据(单位:千克)全部介于![]() 至
至![]() 之间,将数据分成以下
之间,将数据分成以下![]() 组,第一组
组,第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组,第五组
,第四组,第五组![]() ,得到如图所示的频率分布直方图,现采用分层抽样的方法,从第
,得到如图所示的频率分布直方图,现采用分层抽样的方法,从第![]() 、
、![]() 、
、![]() 组中随机抽取
组中随机抽取![]() 名学生做初检.
名学生做初检.
(Ⅰ)求每组抽取的学生人数.
(Ⅱ)若从![]() 名学生中再次随机抽取
名学生中再次随机抽取![]() 名学生进行复检,求这
名学生进行复检,求这![]() 名学生不在同一组的概率.
名学生不在同一组的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,且
,且![]() .
.

(Ⅰ)若点![]() 为
为![]() 上一点且
上一点且![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着高等级公路的迅速发展,公路绿化受到高度重视,需要大量各种苗木.某苗圃培植场对100棵“天竺桂”的移栽成活量![]() (单位:棵)与在前三个月内浇水次数
(单位:棵)与在前三个月内浇水次数![]() 间的关系进行研究,根据以往的记录,整理相关的数据信息如图所示:
间的关系进行研究,根据以往的记录,整理相关的数据信息如图所示:

(1)结合图中前4个矩形提供的数据,利用最小二乘法求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)用![]() 表示(1)中所求的回归直线方程得到的100棵“天竺桂”的移栽成活量的估计值,当图中余下的矩形对应的数据组
表示(1)中所求的回归直线方程得到的100棵“天竺桂”的移栽成活量的估计值,当图中余下的矩形对应的数据组![]() 的残差的绝对值
的残差的绝对值![]() ,则回归直线方程有参考价值,试问:(1)中所得到的回归直线方程有参考价值吗?
,则回归直线方程有参考价值,试问:(1)中所得到的回归直线方程有参考价值吗?
(3)预测100棵“天竺桂”移栽后全部成活时,在前三个月内浇水的最佳次数.
附:回归直线方程为![]() ,其中
,其中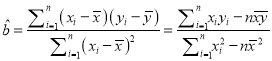 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com