【题目】设函数f(x)的定义域为D，如果x∈D，y∈D，使得f(x)＝－f(y)成立，则称函数f(x)为“Ω函数”．给出下列四个函数：①y＝sin x；②y＝2x；③y＝；④f(x)＝ln x．则其中“Ω函数”共有(　　)

A. 1个 B. 2个 C. 3个 D. 4个

(1)若不等式f(x)≤－5的解集非空，求实数a的取值范围；

(2)若函数y＝f(x)的图象关于点对称，求实数a的值.

【题目】在直角坐标系xOy中，直线l的参数方程为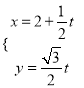 (t为参数)，若以该直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρsin2θ－4cos θ＝0.

(1)求直线l与曲线C的普通方程；

(2)已知直线l与曲线C交于A，B两点，设M(2，0)，求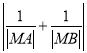的值.

【题目】已知椭圆C： 的左、右焦点为F1，F2，设点F1，F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.

(1)求椭圆C的标准方程；

(2)设A，B，P为椭圆C上三点，满足，记线段AB中点Q的轨迹为E，若直线l：y＝x＋1与轨迹E交于M，N两点，求|MN|.

e＝2.71 828…).

(1)若y＝f(x)在x＝1处的切线方程为y＝2ex＋b，求a，b的值.

(2)若函数f(x)在区间上单调递减，求实数a的取值范围.

（Ⅰ）在所有参与调查的人中，用分层抽样的方法抽取部分市民做进一步调研（不同态度的群体中亦按年龄分层抽样），已知从“保留”态度的人中抽取了19人，则在“支持”态度的群体中，年龄在30岁以上的人有多少人被抽取；

（Ⅱ）在持“不支持”态度的人中，用分层抽样的方法抽取6人做进一步的调研，将此6人看作一个总体，在这6人中任意选取2人，求至少有1人在30岁以上的概率．

【题目】如图，四棱锥P－ABCD中，AP⊥平面PCD，AD∥BC，AB＝BC＝AD，E，F分别为线段AD，PC的中点.

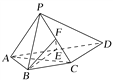
(1)求证：AP∥平面BEF；

(2)求证：BE⊥平面PAC.

(1)求数列{an}，{bn}的通项公式；

(2)设cn＝anbn，求数列{cn}的前n项和Tn.

【题目】已知a，b分别是△ABC内角A，B的对边，且bsin2A＝acos Asin B，函数f(x)＝sin Acos2x－sin2sin 2x，x∈.

(1)求A；

(2)求函数f(x)的值域.

【题目】(2017·合肥市质检)已知点F为椭圆E： (a>b>0)的左焦点，且两焦点与短轴的一个顶点构成一个等边三角形，直线与椭圆E有且仅有一个交点M.

(1)求椭圆E的方程；

(2)设直线与y轴交于P，过点P的直线l与椭圆E交于不同的两点A，B，若λ|PM|2＝|PA|·|PB|，求实数λ的取值范围．