某老师为了分析学生的学习情况，随机抽取了班上20名学生某次期末考试的成绩(满分为150分)进行分析，统计如下：

男生：133　131　130　126　123　120　116　109　107　105

女生：136　127　125　123　119　118　117　114　113　108

(Ⅰ)计算男、女生成绩的平均值并分析比较男、女生成绩的分散程度；

(Ⅱ)现从分数在120分以下的女同学中随机抽取2位，求这两位同学分数之差的绝对值小于10的概率．

在△ABC中，内角A，B，C的对边分别为a，b，c，已知，且b＝5，acos C＝－1.

(Ⅰ)求角A；

(Ⅱ)求△ABC的面积．

【题目】(导学号：05856301)已知函数f(x)＝m(x－1)ex＋x2(m∈R)，其导函数为f′(x)，若对任意的x<0，不等式x2＋(m＋1)x>f′(x)恒成立，则实数m的取值范围为(　　)

A. (0,1) B. (－∞，1) C. (－∞，1] D. (1，＋∞)

【题目】(导学号：05856299)已知双曲线 (a>0，b>0)的左、右焦点分别是F1，F2，点P是其上一点，双曲线的离心率是2，若△F1PF2是直角三角形且面积为3，则双曲线的实轴长为(　　)

A. 2 B. C. 2或 D. 1或

【题目】(导学号：05856295)德国大数学家高斯年少成名，被誉为数学王子.19岁的高斯得到了一个数学史上非常重要的结论，就是《正十七边形尺规作图之理论与方法》， 在其年幼时，对1＋2＋3＋…＋100的求和运算中，提出了倒序相加法的原理，该原理基于所给数据前后对应项的和呈现一定的规律生成，因此，此方法也被称为高斯算法．现有函数f(x)＝，则f(1)＋f(2)＋…＋f(m＋2017)等于(　　)

A. B. C. D.

【题目】已知曲线上任意一点到的距离比到轴的距离大1，椭圆的中心在原点，一个焦点与的焦点重合，长轴长为4．

（Ⅰ）求曲线和椭圆的方程；

（Ⅱ）椭圆上是否存在一点，经过点作曲线的两条切线（为切点）使得直线过椭圆的上顶点，若存在，求出切线的方程，不存在，说明理由．

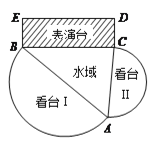
【题目】在一水域上建一个演艺广场.演艺广场由看台Ⅰ，看台Ⅱ，三角形水域，及矩形表演台四个部分构成（如图）.看台Ⅰ，看台Ⅱ是分别以， 为直径的两个半圆形区域，且看台Ⅰ的面积是看台Ⅱ的面积的3倍；矩形表演台中， 米；三角形水域的面积为平方米.设.

（Ⅰ）当时，求的长；

（Ⅱ）若表演台每平方米的造价为万元，求表演台的最低造价.

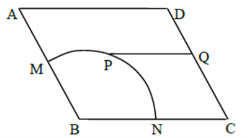
【题目】如图，某广场中间有一块边长为2百米的菱形状绿化区，其中是半径为1百米的扇形，． 管理部门欲在该地从到修建小路：在弧上选一点（异于两点），过点修建与平行的小路．问：点选择在何处时，才能使得修建的小路与及的总长最小？并说明理由．

(1)求数列{an}的通项公式；

(2)若数列{bn}满足an＋1＝，Tn为数列{bn}的前n项和，若Tn≥m恒成立，求m的最大值.

A. S2 016＝－2 016，a2 013>a4

B. S2 016＝2 016，a2 013>a4

C. S2 016＝－2 016，a2 013<a4

D. S2 016＝2 016，a2 013<a4