
科目: 来源: 题型:
【题目】以下命题:①根据斜二测画法,三角形的直观图是三角形;②有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱;③两相邻侧面所成角相等的棱锥是正棱锥;④若两个二面角的半平面互相垂直,则这两个二面角的大小相等或互补.其中正确命题的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人轮流投篮,每人每次投一次篮,先投中者获胜.投篮进行到有人获胜或每人都已投球3次时结束.设甲每次投篮命中的概率为![]() ,乙每次投篮命中的概率为
,乙每次投篮命中的概率为![]() ,且各次投篮互不影响.现由甲先投.
,且各次投篮互不影响.现由甲先投.
(1)求甲获胜的概率;
(2)求投篮结束时甲的投篮次数X的分布列与期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(I)若曲线![]() ,参数方程为:
,参数方程为:![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程
的普通方程
(Ⅱ)若曲线![]() ,参数方程为
,参数方程为![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() ,与曲线
,与曲线![]() 交点分别为
交点分别为![]() ,求
,求![]() 的取值范围,
的取值范围,
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB,且AB![]() BP
BP![]() 2,AD=AE=1,AE⊥AB,且AE∥BP.
2,AD=AE=1,AE⊥AB,且AE∥BP.

(1)求平面PCD与平面ABPE所成的二面角的余弦值;
(2)线段PD上是否存在一点N,使得直线BN与平面PCD所成角的正弦值等于![]() ?若存在,试确定点N的位置;若不存在,请说明理由.
?若存在,试确定点N的位置;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】祖暅原理:两个等高的几何体,若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.利用祖暅原理可以求旋转体的体积.比如:设半圆方程为![]() ,半圆与
,半圆与![]() 轴正半轴交于点
轴正半轴交于点![]() ,作直线
,作直线![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() (
(![]() 为原点),利用祖暅原理可得:半圆绕
为原点),利用祖暅原理可得:半圆绕![]() 轴旋转所得半球的体积与
轴旋转所得半球的体积与![]() 绕
绕![]() 轴旋转一周形成的几何体的体积相等.类比这个方法,可得半椭圆
轴旋转一周形成的几何体的体积相等.类比这个方法,可得半椭圆![]() 绕
绕![]() 轴旋转一周形成的几何体的体积是_________.
轴旋转一周形成的几何体的体积是_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】新个税法于2019年1月1日进行实施.为了调查国企员工对新个税法的满意程度,研究人员在![]() 地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中
地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.
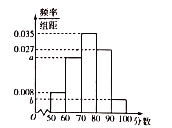
(1)求![]() 的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
的值并估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
(2)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】有甲、乙两队学生参加“知识联想”抢答赛,比赛规则:①主持人依次给出两次提示,第一次提示后答对得2分,第二次提示后答对得1分,没抢到或答错者不得分;②主持人给出第一个提示后开始抢答,第一轮抢答出错失去第二轮答题资格;③每局比赛分两轮,若第一轮抢答者给出正确答案,则此局比赛结束,若第一轮答题者答错,主持人提示后另一队直接答题。如果甲、乙两队抢到答题权机会均等,并且势均力敌,第一个提示后答对概率均为![]() ;第二个提示后答对概率均为
;第二个提示后答对概率均为![]() ,
,![]() 为甲队在一局比赛中的分.
为甲队在一局比赛中的分.
(1)求甲在一局比赛中得分的分布列;
(2)若比赛共4局,求甲4局比赛中至少得6分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com