
科目: 来源: 题型:
【题目】2017年11月、12月全国大范围流感爆发,为研究昼夜温差大小与患感冒人数多少之间的关系,一兴趣小组抄录了某医院11月到12月间的连续6个星期的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期 | 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | 第六周 |
昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验。
(Ⅰ)求选取的2组数据恰好是相邻两个星期的概率;
(Ⅱ)若选取的是第一周与第六周的两组数据,请根据第二周到第五周的4组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式: 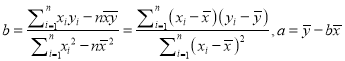 )
)
参考数据: ![]() 1092,
1092, ![]() 498
498
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解学生的课外阅读时间情况,某学校随机抽取了 50人进行统计分析,把这50人每天阅读的时间(单位:分钟)绘制成频数分布表,如下表所示:

若把每天阅读时间在60分钟以上(含60分钟)的同学称为“阅读达人”,根据统计结果中男女生阅读达人的数据,制作出如图所示的等高条形图.
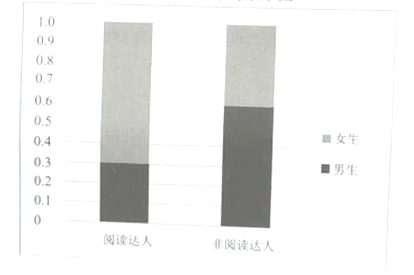
(1)根据抽样结果估计该校学生的每天平均阅读时间(同一组数据用该区间的中点值作为代表);
(2)根据已知条件完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“阅读达人”跟性别有关?
的把握认为“阅读达人”跟性别有关?
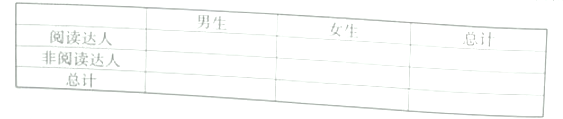
附:参考公式
![]() ,其中
,其中![]() .
.
临界值表:
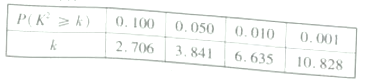
查看答案和解析>>
科目: 来源: 题型:
【题目】矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,将
中点,将![]() 沿
沿![]() 所在直线翻折,在翻折过程中,给出下列结论:
所在直线翻折,在翻折过程中,给出下列结论:
①存在某个位置,![]() ; ②存在某个位置,
; ②存在某个位置,![]() ;
;
③存在某个位置,![]() ; ④存在某个位置,
; ④存在某个位置,![]() .
.
其中正确的是( )
A. ①② B. ③④ C. ①③ D. ②④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)是定义域为R上的奇函数,当x>0时,f(x)=x2+2x.
(1)求f(x)的解析式;
(2)若不等式f(t﹣2)+f(2t+1)>0成立,求实数t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年,随着中国第一款5G手机投入市场,5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析,得到如下规律:每生产手机![]() 万台,其总成本为
万台,其总成本为![]() ,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入
,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入![]() 万元满足
万元满足
(1)将利润![]() 表示为产量
表示为产量![]() 万台的函数;
万台的函数;
(2)当产量![]() 为何值时,公司所获利润最大?最大利润为多少万元?
为何值时,公司所获利润最大?最大利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com