【题目】已知点，，在圆E上，过点的直线l与圆E相切．

Ⅰ求圆E的方程；

Ⅱ求直线l的方程．

【题目】设椭圆E的方程为 (a>b>0)，点O为坐标原点，点A的坐标为(a，0)，点B的坐标为(0，b)，点M在线段AB上，满足BM＝2MA，直线OM的斜率为.

(1)求E的离心率e；

(2)设点C的坐标为(0，－b)，N为线段AC的中点，点N关于直线AB的对称点的纵坐标为，求E的方程.

【题目】如图，摩天轮上的一点在时刻距离地面的高度满足，已知该摩天轮的半径为60米，摩天轮转轮中心O距离地面的高度是70米，摩天轮逆时针做匀速转动，每6分钟转一圈，点的起始位置在摩天轮的最低点处.

（1）根据条件求出y（米）关于（分钟）的解析式；

（2）在摩天轮从最低点开始计时转动的一圈内，有多长时间点P距离地面不低于100米？

【题目】某车间有5名工人其中初级工2人，中级工2人，高级工1人现从这5名工人中随机抽取2名．

Ⅰ求被抽取的2名工人都是初级工的概率；

Ⅱ求被抽取的2名工人中没有中级工的概率．

【题目】如图，在平面直角坐标系xOy中，已知椭圆过点A(2，1)，离心率为．

（Ⅰ）求椭圆的方程；

（Ⅱ）若直线与椭圆相交于B，C两点(异于点A)，线段BC被y轴平分，且，求直线l的方程．

【题目】已知ω＞0，0＜φ＜π，直线和是函数f（x）＝sin（ωx+φ）图象的两条相邻的对称轴，若将函数f（x）图象上每一点的横坐标变为原来的倍，纵坐标变为原来的2倍，则得到的图象的函数解析式是（ ）

A.B.

C.y＝2cos2xD.

【题目】如图所示的几何体中，平面ABCD，四边形ABCD为菱形，，点M，N分别在棱FD，ED上.

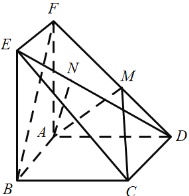
（1）若平面MAC，设，求的值；

（2）若，平面AEN平面EDC所成的锐二面角为，求BE的长.

在直角坐标系中，以原点为极点， 轴的非负半轴为极轴建立极坐标系，已知曲线的极坐标方程为，过点的直线（为参数）与曲线相交于两点．

（1）试写出曲线的直角坐标方程和直线的普通方程；

（2）求的值．

(1)求图中a的值;

(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;

(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.

【题目】某校为了解高二年级学生某次数学考试成绩的分布情况，从该年级的1120名学生中随机抽取了100名学生的数学成绩，发现都在内现将这100名学生的成绩按照，，，，，，分组后，得到的频率分布直方图如图所示,则下列说法正确的是　　

A. 频率分布直方图中a的值为

B. 样本数据低于130分的频率为

C. 总体的中位数保留1位小数估计为分

D. 总体分布在的频数一定与总体分布在的频数相等