
科目: 来源: 题型:
【题目】某大型超市在2018年元旦举办了一次抽奖活动,抽奖箱里放有2个红球,1个黄球和1个蓝球(这些小球除颜色外大小形状完全相同),从中随机一次性取2个小球,每位顾客每次抽完奖后将球放回抽奖箱.活动另附说明如下:
①凡购物满100(含100)元者,凭购物打印凭条可获得一次抽奖机会;
②凡购物满188(含188)元者,凭购物打印凭条可获得两次抽奖机会;
③若取得的2个小球都是红球,则该顾客中得一等奖,奖金是一个10元的红包;
④若取得的2个小球都不是红球,则该顾客中得二等奖,奖金是一个5元的红包;
⑤若取得的2个小球只有1个红球,则该顾客中得三等奖,奖金是一个2元的红包.
抽奖活动的组织者记录了该超市前20位顾客的购物消费数据(单位:元),绘制得到如图所示的茎叶图.

(1)求这20位顾客中获得抽奖机会的人数与抽奖总次数(假定每位获得抽奖机会的顾客都会去抽奖);
(2)求这20位顾客中奖得抽奖机会的顾客的购物消费数据的中位数与平均数(结果精确到整数部分);
(3)分别求在一次抽奖中获得红包奖金10元,5元,2元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列结论正确的是( )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.
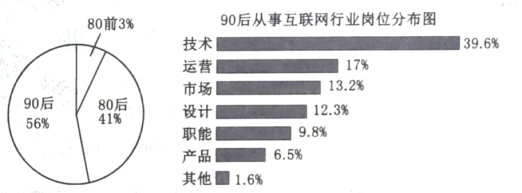
A.互联网行业从业人员中从事技术和运营岗位的人数占总人数的三成以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目: 来源: 题型:
【题目】若函数![]() 对定义域内的每一个值
对定义域内的每一个值![]() ,在其定义域内都存在唯一的
,在其定义域内都存在唯一的![]() ,使
,使![]() 成立,则称该函数为“
成立,则称该函数为“![]() 函数”.
函数”.
(1)判断函数![]() 是否为“
是否为“![]() 函数”,并说明理由;
函数”,并说明理由;
(2)若函数![]() 在定义域
在定义域![]() 上是“
上是“![]() 函数”,求
函数”,求![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在定义域
在定义域![]() 上为“
上为“![]() 函数”.若存在实数
函数”.若存在实数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 都成立,求实数
都成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆的方程;
(2)A是椭圆与y轴正半轴的交点,椭圆上是否存在两点M,N,使得△AMN是以A为直角顶点的等腰直角三角形?若存在,请说明有几个,并求出直线MN;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,抛物线
,抛物线![]() :
: ![]() 与抛物线
与抛物线![]() :
: ![]() 异于原点
异于原点![]() 的交点为
的交点为![]() ,且抛物线
,且抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)若直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,
, ![]() ,且
,且![]() ,求抛物线
,求抛物线![]() 的方程;
的方程;
(2)证明: ![]() 的面积与四边形
的面积与四边形![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上.
上.
(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某大型超市在2018年元旦举办了一次抽奖活动,抽奖箱里放有2个红球,1个黄球和1个蓝球(这些小球除颜色外大小形状完全相同),从中随机一次性取2个小球,每位顾客每次抽完奖后将球放回抽奖箱.活动另附说明如下:
①凡购物满100(含100)元者,凭购物打印凭条可获得一次抽奖机会;
②凡购物满188(含188)元者,凭购物打印凭条可获得两次抽奖机会;
③若取得的2个小球都是红球,则该顾客中得一等奖,奖金是一个10元的红包;
④若取得的2个小球都不是红球,则该顾客中得二等奖,奖金是一个5元的红包;
⑤若取得的2个小球只有1个红球,则该顾客中得三等奖,奖金是一个2元的红包.
抽奖活动的组织者记录了该超市前20位顾客的购物消费数据(单位:元),绘制得到如图所示的茎叶图.

(1)求这20位顾客中获得抽奖机会的人数与抽奖总次数(假定每位获得抽奖机会的顾客都会去抽奖);
(2)求这20位顾客中奖得抽奖机会的顾客的购物消费数据的中位数与平均数(结果精确到整数部分);
(3)分别求在一次抽奖中获得红包奖金10元,5元,2元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com