
科目: 来源: 题型:
【题目】已知数列{an}中,点(an,an+1)在直线y=x+2上,且首项a1=1.
(1)求数列{an}的通项公式;
(2)数列{an}的前n项和为Sn,等比数列{bn}中,b1=a1,b2=a2,数列{bn}的前n项和为Tn,请写出适合条件Tn≤Sn的所有n的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等差数列{an}的各项均为正数,a1=1,前n项和为Sn.数列{bn}为等比数列,b1=1,且b2S2=6,b2+S3=8.
(1)求数列{an}与{bn}的通项公式;
(2)求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,且a1=1,S3+S4=S5.
(1)求数列{an}的通项公式;
(2)令bn=(-1)n-1an,求数列{bn}的前2n项和T2n.
查看答案和解析>>
科目: 来源: 题型:
【题目】某网站举行“卫生防疫”的知识竞赛网上答题,共有120000人通过该网站参加了这次竞赛,为了解竞赛成绩情况,从中抽取了100人的成绩进行统计,其中成绩分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:
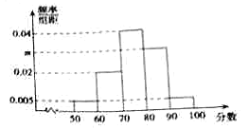
(1)求![]() 的值;
的值;
(2)成绩不低于90分的人就能获得积分奖励,求所有参赛者中获得奖励的人数;
(3)根据频率分布直方图,估计这次知识竞赛成绩的平均分(用组中值代替各组数据的平均值).
查看答案和解析>>
科目: 来源: 题型:
【题目】(题文)某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验数据统计如下:
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
A | 甲 | 4次 | 6次 | 2次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,请你根据人工降雨模拟实验的统计数据:
(1)求甲、乙、丙三地都恰为中雨的概率;
(2)考虑到旱情和水土流失,如果甲地恰需中雨即达到理想状态,乙地必须是大雨才达到理想状态,丙地只要是小雨或中雨即达到理想状态,记“甲、乙、丙三地中达到理想状态的个数”为随机变量ξ,求随机变量ξ的分布列和均值E(ξ).
查看答案和解析>>
科目: 来源: 题型:
【题目】剪纸艺术是最古老的中国民间艺术之一,作为一种镂空艺术,它能给人以视觉上以透空的感觉和艺术享受.在中国南北方的剪纸艺术,通过一把剪刀、一张纸、就可以表达生活中的各种喜怒哀乐.如图是一边长为1的正方形剪纸图案,中间黑色大圆与正方形的内切圆共圆心,圆与圆之间是相切的,且中间黑色大圆的半径是黑色小圆半径的2倍,若在正方形图案上随机取一点,则该点取自白色区域的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 网络是一种先进的高频传输技术,我国的
网络是一种先进的高频传输技术,我国的![]() 技术发展迅速,已位居世界前列.华为公司2019年8月初推出了一款
技术发展迅速,已位居世界前列.华为公司2019年8月初推出了一款![]() 手机,现调查得到该款
手机,现调查得到该款![]() 手机上市时间
手机上市时间![]() 和市场占有率
和市场占有率![]() (单位:%)的几组相关对应数据.如图所示的折线图中,横轴1代表2019年8月,2代表2019年9月……,5代表2019年12月,根据数据得出
(单位:%)的几组相关对应数据.如图所示的折线图中,横轴1代表2019年8月,2代表2019年9月……,5代表2019年12月,根据数据得出![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .若用此方程分析并预测该款手机市场占有率的变化趋势,则最早何时该款
.若用此方程分析并预测该款手机市场占有率的变化趋势,则最早何时该款![]() 手机市场占有率能超过0.5%(精确到月)( )
手机市场占有率能超过0.5%(精确到月)( )

A.2020年6月B.2020年7月C.2020年8月D.2020年9月
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂拟建一座平面图为矩形,面积为![]() ,高度一定的三段污水处理池(如图),由于受地形限制,其长、宽都不超过
,高度一定的三段污水处理池(如图),由于受地形限制,其长、宽都不超过![]() ,如果池的外壁的建造费单价为
,如果池的外壁的建造费单价为![]() 元
元![]() ,池中两道隔壁墙(与宽边平行)的建造费单价为
,池中两道隔壁墙(与宽边平行)的建造费单价为![]() 元
元![]() ,池底的建造费单价为
,池底的建造费单价为![]() 元
元![]() .设水池的长为
.设水池的长为![]() ,总造价为
,总造价为![]() .
.

(1)求![]() 的表达式;
的表达式;
(2)水池的长与宽各是多少时,总造价最低,并求出这个最低造价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com