
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,经过点
中,经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() 和
和![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)设椭圆与![]() 轴正半轴、
轴正半轴、![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,是否存在常数
,是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求
共线?如果存在,求![]() 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】朱世杰是历史上最伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题:“今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升,共支米四百三石九斗二升,问筑堤几日”。其大意为“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人,修筑堤坝的每人每天分发大米3升,共发出大米40392升,问修筑堤坝多少天”,在该问题中前5天共分发了多少大米?
A. 1170升 B. 1380升 C. 3090升 D. 3300升
查看答案和解析>>
科目: 来源: 题型:
【题目】一半径为![]() 米的水轮如图所示,水轮圆心
米的水轮如图所示,水轮圆心![]() 距离水面
距离水面![]() 米;已知水轮按逆时针做匀速转动,每
米;已知水轮按逆时针做匀速转动,每![]() 秒转一圈,如果当水轮上点
秒转一圈,如果当水轮上点![]() 从水中浮现时(图中点
从水中浮现时(图中点![]() )开始计算时间.
)开始计算时间.

(1)以水轮所在平面与水面的交线为![]() 轴,以过点
轴,以过点![]() 且与水面垂直的直线为
且与水面垂直的直线为![]() 轴,建立如图所示的直角坐标系,试将点
轴,建立如图所示的直角坐标系,试将点![]() 距离水面的高度
距离水面的高度![]() (单位:米)表示为时间
(单位:米)表示为时间![]() (单位:秒)的函数;
(单位:秒)的函数;
(2)在水轮转动的任意一圈内,有多长时间点![]() 距水面的高度超过
距水面的高度超过![]() 米?
米?
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4 — 4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为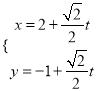 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ).
).
(1)分别写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为![]() 的直线
的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于
的圆交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
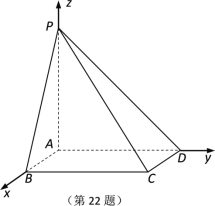
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若点M,N分别在AB,PC上,且![]() 平面
平面![]() ,试确定点M,N的位置.
,试确定点M,N的位置.
查看答案和解析>>
科目: 来源: 题型:
【题目】某课题小组共10人,已知该小组外出参加交流活动次数为1,2,3的人数分别为3,3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.
(1)记“选出2人外出参加交流活动次数之和为4”为事件A,求事件A发生的概率;
(2)设X为选出2人参加交流活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com