
科目: 来源: 题型:
【题目】(1)![]() 人坐在有八个座位的一排上,若每人的左右两边都要有空位,则不同坐法的种数有多少种?
人坐在有八个座位的一排上,若每人的左右两边都要有空位,则不同坐法的种数有多少种?
(2)有![]() 个人并排站成一排,如果甲必须在乙的右边,则不同的排法有多少种?
个人并排站成一排,如果甲必须在乙的右边,则不同的排法有多少种?
(3)现有![]() 个保送上大学的名额,分配给
个保送上大学的名额,分配给![]() 所学校,每校至少有一个名额,问:名额分配的方法共有多少种?
所学校,每校至少有一个名额,问:名额分配的方法共有多少种?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥PABCD中,侧面PAD是正三角形,底面ABCD是菱形,且∠ABC=60°,M为PC的中点.
(1)求证:PC⊥AD.
(2)在棱PB上是否存在一点Q,使得A,Q,M,D四点共面?若存在,指出点Q的位置并证明;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】对于函数f(x),若f(x)的图象上存在关于原点对称的点,则称f(x)为定义域上的“伪奇函数”.
(1)若f(x)=ln(2x+1)+m是定义在区间[﹣1,1]上的“伪奇函数”,求实数m的取值范围;
(2)试讨论f(x)=4x﹣m2x+2+4m2﹣3在R上是否为“伪奇函数”?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地有一企业2007年建厂并开始投资生产,年份代号为7,2008年年份代号为8,依次类推.经连续统计9年的收入情况如下表(经数据分析可用线性回归模型拟合![]() 与
与![]() 的关系):
的关系):
年份代号( | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
当年收入( | 13 | 14 | 18 | 20 | 21 | 22 | 24 | 28 | 29 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)试预测2020年该企业的收入.
(参考公式: 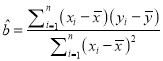
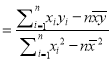 ,
, ![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在正方体ABCDA1B1C1D1中,M,N分别是棱AB,CC1的中点,△MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:

①平面MB1P⊥ND1;
②平面MB1P⊥平面ND1A1;
③△MB1P在底面ABCD上的射影图形的面积为定值;
④△MB1P在侧面DD1C1C上的射影图形是三角形.
其中正确的命题序号是( )
A. ①B. ②③
C. ①③D. ②④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,如图1.已知
,如图1.已知![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() .
.


(1)求抛物线![]() 的方程;
的方程;
(2)若正方形![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 都在抛物线
都在抛物线![]() 上(如图2),求正方形
上(如图2),求正方形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两所学校进行同一门课程的考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下![]() 列联表:
列联表:
班级与成绩列联表
优秀 | 不优秀 | 总计 | |
甲队 | 80 | 40 | 120 |
乙队 | 240 | 200 | 240 |
合计 | 320 | 240 | 560 |
(1)能否在犯错误的概率不超过0.025的前提下认为成绩与学校有关系;
(2)采用分层抽样的方法在两所学校成绩优秀的320名学生中抽取16名同学.现从这16名同学中随机抽取3名运同学作为成绩优秀学生代表介绍学习经验,记这3名同学来自甲学校的人数为![]() ,求
,求![]() 的分布列与数学期望.附:
的分布列与数学期望.附:
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com