
科目: 来源: 题型:
【题目】(多选题)在数列![]() 中,若
中,若![]() ,(
,(![]() ,
,![]() ,
,![]() 为常数),则称
为常数),则称![]() 为“等方差数列”.下列对“等方差数列”的判断正确的是( )
为“等方差数列”.下列对“等方差数列”的判断正确的是( )
A.若![]() 是等差数列,则
是等差数列,则![]() 是等方差数列
是等方差数列
B.![]() 是等方差数列
是等方差数列
C.若![]() 是等方差数列,则
是等方差数列,则![]() (
(![]() ,
,![]() 为常数)也是等方差数列
为常数)也是等方差数列
D.若![]() 既是等方差数列,又是等差数列,则该数列为常数列
既是等方差数列,又是等差数列,则该数列为常数列
查看答案和解析>>
科目: 来源: 题型:
【题目】某经销商计划销售一款新型的电子产品,经市场调研发现以下规律:当每台电子产品的利润为x(单位:元,x>0)时,销售量q(x)(单位:百台)与x的关系满足:若x不超过25,则q(x)=![]() ;若x大于或等于225,则销售量为零;当25≤x≤225时,q(x)=a-b
;若x大于或等于225,则销售量为零;当25≤x≤225时,q(x)=a-b![]() (a,b为实常数).
(a,b为实常数).
(1) 求函数q(x)的表达式;
(2) 当x为多少时,总利润(单位:元)取得最大值,并求出该最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】手机是人们必不可少的工具,极大地方便了人们的生活、工作、学习,现代社会的衣食住行都离不开它.某调查机构调查了某地区各品牌手机的线下销售情况,将数据整理得如下表格:
品牌 |
|
|
|
|
|
| 其他 |
销售比 |
|
|
|
|
|
|
|
每台利润(元) | 100 | 80 | 85 | 1000 | 70 | 200 |
该地区某商场岀售各种品牌手机,以各品牌手机的销售比作为各品牌手机的售出概率.
(1)此商场有一个优惠活动,每天抽取一个数字![]() (
(![]() ,且
,且![]() ),规定若当天卖出的第
),规定若当天卖出的第![]() 台手机恰好是当天卖出的第一台
台手机恰好是当天卖出的第一台![]() 手机时,则此
手机时,则此![]() 手机可以打5折.为保证每天该活动的中奖概率小于0.05,求
手机可以打5折.为保证每天该活动的中奖概率小于0.05,求![]() 的最小值;(
的最小值;(![]() ,
,![]() )
)
(2)此商场中一个手机专卖店只出售![]() 和
和![]() 两种品牌的手机,
两种品牌的手机,![]() ,
,![]() 品牌手机的售出概率之比为
品牌手机的售出概率之比为![]() ,若此专卖店一天中卖出3台手机,其中
,若此专卖店一天中卖出3台手机,其中![]() 手机
手机![]() 台,求
台,求![]() 的分布列及此专卖店当天所获利润的期望值.
的分布列及此专卖店当天所获利润的期望值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 的圆心为原点,其半径与椭圆
的圆心为原点,其半径与椭圆![]() 的左焦点和上顶点的连线线段长度相等.
的左焦点和上顶点的连线线段长度相等.
(1)求圆![]() 的标准方程;
的标准方程;
(2)过椭圆右焦点的动直线![]() (其斜率不为0)交圆
(其斜率不为0)交圆![]() 于
于![]() 两点,试探究在
两点,试探究在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之和为0?若存在,求出点
的斜率之和为0?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=loga(1+![]() x),g(x)=loga(1-
x),g(x)=loga(1-![]() x),(a>0且a≠1),若h(x)=f(x)-g(x).
x),(a>0且a≠1),若h(x)=f(x)-g(x).
(1)求函数h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若f(2)=1,求使h(x)>0成立的x的集合.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司在某条商业街分别开有两家业务上有关联的零售商店,这两家商店的日纯利润变化情况如下表所示:

(1)从这几天的日纯利润来看,哪一家商店的日平均纯利润多些?
(2)由表中数据可以认为这两家商店的日纯利润之间有较强的线性相关关系.
(ⅰ)试求![]() 与
与![]() 之间的线性回归方程;
之间的线性回归方程;
(ⅱ)预测当![]() 店日纯利润不低于2万元时,
店日纯利润不低于2万元时,![]() 店日纯利润的大致范围(精确到小数点后两位);
店日纯利润的大致范围(精确到小数点后两位);
(3)根据上述5日内的日纯利润变化情况来看,哪家商店经营状况更好?
附:线性回归方程![]() 中,
中,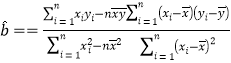 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】设命题p:实数![]() 满足不等式
满足不等式![]() ;
;
命题q:关于![]() 不等式
不等式![]() 对任意的
对任意的![]() 恒成立.
恒成立.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的参数方程;
的参数方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,抛物线
中,抛物线![]() 的方程为
的方程为![]() ,以点
,以点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求直线![]() 的直角坐标方程,点
的直角坐标方程,点![]() 的极坐标;
的极坐标;
(2)设![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com